题目内容
9.为了解决停车难问题,交通部门准备沿12米宽60米长的道路边规划停车位,按每辆车长5米、宽2.4米设计停车后道路仍有不少于7米的路宽保证两车可以双向通过,如下图设计方案1:车位长边与路边夹角为45°方案2:车位长边与路边夹角为30°(1)请计算说明,两种方案是否都能保证通行要求?
(2)计算符合通行要求的方案中最多可以停多少辆车?
(3)请你画示意图设计一个满足通行要求且停车更多的新方案,并计算出最多停放车辆数.

分析 (1)根据正弦函数求得AB、AE的长,进而求得BE的长,即可判定方案是否能保证通行要求;
(2)根据正弦函数和余弦函数求得方案2中的MB的长,即可求得此方案中最多可以停多少辆车;
(3)如图所示新方案,根据车的宽度即可计算出最多停放车辆数.
解答 解:(1)方案1:
如图,AB=2.4×sin45°=2.4×$\frac{\sqrt{2}}{2}$≈1.54米,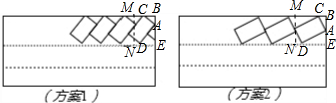
AE=5×sin45°=5×$\frac{\sqrt{2}}{2}$≈3.5米,
BE=AB+AE≈5.04,
∵12-5.04=<7,
∴方案1不能保证通行要求;
方案2:
AB=2.4×cos30°=2.4×$\frac{\sqrt{3}}{2}$≈2.1米,
AE=5×sin30°=5×$\frac{1}{2}$=2.5米,
BE=AB+AE=2.1+2.5=4.6,
∵12-4.6=7.4>7,
∴方案2能保证通行要求;
(2)BC=2.4×sin30°=2.4×$\frac{1}{2}$=1.2米,
MC=5×cos30°=5×$\frac{\sqrt{3}}{2}$≈4.3米,
MB=BC+MC=1.2+4.3=5.5,
60÷5.5=10.9(辆).
故方案2中最多可以停10辆车.
(3)新方案如图: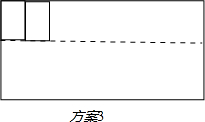
60÷2.4=25(辆).
故这个方案最多可以停放25辆车.
点评 本题考查了学生利用三角函数解决实际问题的能力以及矩形的性质.这就要求学生把实际问题转化为直角三角形的问题,利用三角函数解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知?ABCD的周长为36cm,过点A作AE⊥BC,AF⊥CD,若AE=2cm,AF=4cm,求平行四边形各边的长.
已知?ABCD的周长为36cm,过点A作AE⊥BC,AF⊥CD,若AE=2cm,AF=4cm,求平行四边形各边的长.
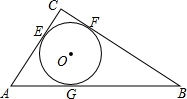 在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.如图,⊙O是△ABC的内切圆,与三边分别相切于点E、F、G.
在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.如图,⊙O是△ABC的内切圆,与三边分别相切于点E、F、G. 如图,两条平行线AB、CD被直线BC所截,一组同旁内角的平分线相交于点E,则∠BEC的度数是90°.
如图,两条平行线AB、CD被直线BC所截,一组同旁内角的平分线相交于点E,则∠BEC的度数是90°. 如图,△ABC是等边三角形,若点A绕点C顺时针旋转30°至点A′,联结A′B,则∠ABA′度数是15°.
如图,△ABC是等边三角形,若点A绕点C顺时针旋转30°至点A′,联结A′B,则∠ABA′度数是15°.