题目内容
1. 如图,两条平行线AB、CD被直线BC所截,一组同旁内角的平分线相交于点E,则∠BEC的度数是90°.
如图,两条平行线AB、CD被直线BC所截,一组同旁内角的平分线相交于点E,则∠BEC的度数是90°.
分析 先根据平行线的性质得出∠ABC+∠BCD=180°,再由角平分线的性质得出∠EBC+∠EDB=90°,再根据三角形内角和定理即可得出结论.
解答 解:∵AB∥CD,
∴∠ABC+∠BCD=180°.
∵一组同旁内角的平分线相交于点E,
∴∠EBC+∠EDB=$\frac{1}{2}$(∠ABC+∠BCD)=90°,
∴∠E=180°-(∠EBC+∠EDB)=180°-90°=90°.
故答案为:90°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.

练习册系列答案
相关题目
6.如图所示,∠2和∠1是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
13.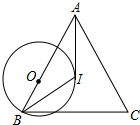 如图,在△ABC中,I是△ABC的内心,O是AB边上一点,⊙O经过B点且与AI相切于I点.若tan∠BAC=$\frac{24}{7}$,则sin∠C的值为( )
如图,在△ABC中,I是△ABC的内心,O是AB边上一点,⊙O经过B点且与AI相切于I点.若tan∠BAC=$\frac{24}{7}$,则sin∠C的值为( )
 如图,在△ABC中,I是△ABC的内心,O是AB边上一点,⊙O经过B点且与AI相切于I点.若tan∠BAC=$\frac{24}{7}$,则sin∠C的值为( )
如图,在△ABC中,I是△ABC的内心,O是AB边上一点,⊙O经过B点且与AI相切于I点.若tan∠BAC=$\frac{24}{7}$,则sin∠C的值为( )| A. | $\frac{5}{6}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{\sqrt{3}}{3}$ |
11.下列语句中不是命题的是( )
| A. | 有理数的混合运算 | B. | 对顶角相等 | ||
| C. | 若∠1=∠2,∠2=∠3,则∠1=∠3 | D. | 任何数的平方都是非负数 |
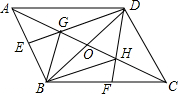 如图,已知G,H是△ABC的边AC的等分点,GE∥BH交AB于E,HF∥BG交BC于F,延长EG、FH交于D点,连接AD、DC、BD.设AC和BD交于O点,求证:四边形ABCD是平行四边形.
如图,已知G,H是△ABC的边AC的等分点,GE∥BH交AB于E,HF∥BG交BC于F,延长EG、FH交于D点,连接AD、DC、BD.设AC和BD交于O点,求证:四边形ABCD是平行四边形.