题目内容
14.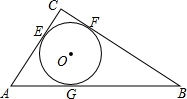 在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.如图,⊙O是△ABC的内切圆,与三边分别相切于点E、F、G.
在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.如图,⊙O是△ABC的内切圆,与三边分别相切于点E、F、G.(1)求证:内切圆的半径r=1;
(2)求tan∠OAG的值.
分析 (1)如图连结OE,OF,OG.由⊙O是△ABC的内切圆,∠C=90°,得到四边形CEOF是正方形,根据切线长定理列方程得到结果;
(2)连结OA,在Rt△AOG中,由锐角三角函数得到结果.
解答  (1)证明:如图连结OE,OF,OG.
(1)证明:如图连结OE,OF,OG.
∵⊙O是△ABC的内切圆,∠C=90°,
∴四边形CEOF是正方形,
∴CE=CF=r.
又∵AG=AE=3-r,BG=BF=4-r,AG+BG=5,
∴(3-r)+(4-r)=5.
解得r=1;
(2)解:连结OA,在Rt△AOG中,
∵r=1,AG=3-r=2,
tan∠OAG=$\frac{OG}{AG}$=$\frac{1}{2}$.
点评 本题考查了三角形的内切圆的性质,切线长定理,锐角三角函数,熟记切线长定理是解题的关键.

练习册系列答案
相关题目
19.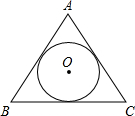 如图,若等边△ABC的内切圆⊙O的半径是2,则△ABC的面积是( )
如图,若等边△ABC的内切圆⊙O的半径是2,则△ABC的面积是( )
 如图,若等边△ABC的内切圆⊙O的半径是2,则△ABC的面积是( )
如图,若等边△ABC的内切圆⊙O的半径是2,则△ABC的面积是( )| A. | 4$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
6.如图所示,∠2和∠1是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
3.要使式子$\frac{{\sqrt{x-1}}}{x}$有意义,x的取值范围是( )
| A. | x≠1 | B. | x≠0 | C. | x>1且x≠0 | D. | x≥1 |
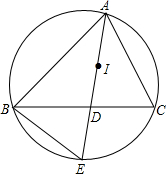 如图,I是△ABC的内心,AI的延长线交边BC于点D,交△ABC的外接圆于点E.
如图,I是△ABC的内心,AI的延长线交边BC于点D,交△ABC的外接圆于点E.