题目内容
11.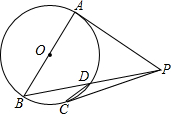 如图,AB是⊙O的直径,PA,PC是⊙O的切线,A,C是切点,PB交⊙O于点D.
如图,AB是⊙O的直径,PA,PC是⊙O的切线,A,C是切点,PB交⊙O于点D.(1)求证:∠APC=2∠BDC;
(2)若CD∥AB,求sin∠BDC的值.
分析 (1)连接AC、OP,交于点E,根据切线长定理得出OA⊥PA,OP⊥AC,∠OPA=∠OPC=$\frac{1}{2}$∠APC,根据圆周角定理得出∠BDC=∠BAC,即可证得结论;
(2)连接AD,CB,过点P作PE⊥CB交BC的延长线于E,由PA、PC是⊙O的切线,得到PA=PC,∠3=∠5,∠1=∠2,由于AB∥CD,得到∠ABC=∠DCE,推出∠3=∠4,∠5=∠4,通过△ADP≌△CPE,得到AD=CE,PD=PE,设PE=PD=a,CE=BC=AD=b,由射影定理得 2a2=b2,由勾股定理得PA=PC=$\sqrt{P{E}^{2}+C{E}^{2}}$=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{3}$a,于是得到结果sin∠BDC=sin∠5=$\frac{PD}{PA}$=$\frac{a}{\sqrt{3}a}$=$\frac{\sqrt{3}}{3}$.
解答 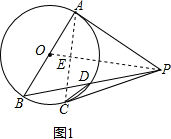 解:(1)连接AC、OP,交于点E,如图1,
解:(1)连接AC、OP,交于点E,如图1,
∵AB是⊙O的直径,PA,PC是⊙O的切线,
∴OA⊥PA,OP⊥AC,∠OPA=∠OPC=$\frac{1}{2}$∠APC,
∵∠AOP=∠EOA,∠AEO=∠PAO=90°,
∴∠BAC=∠OPA=$\frac{1}{2}$∠APC,
∴∠APC=2∠BAC,
∵∠BDC=∠BAC,
∴∠APC=2∠BDC;
(2)连接AD,BC,过点P作PE⊥BC交BC的延长线于E,如图2,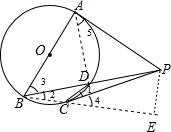
∵PA、PC是⊙O的切线,
∴PA=PC,∠3=∠5,∠1=∠2,
∵CD∥AB,
∴∠ABC=∠DCE,
∴∠3=∠4,
∴∠5=∠4,
在△ADP与△CEP中,
$\left\{\begin{array}{l}{∠ADP=PEC=90°}\\{∠5=∠4}\\{PA=PC}\end{array}\right.$,
∴△ADP≌△CEP,
∴AD=CE,PD=PE,
∵AB∥CD,
∴AD=BC,
设PE=PD=a,CE=BC=AD=b,
∵∠BAP=90°,
由射影定理得:AD2=PD•BD,
∴BD=$\frac{A{D}^{2}}{PD}$=$\frac{{b}^{2}}{a}$,
∴PB=$\frac{{b}^{2}}{a}$+a,BE=2b,
在Rt△PBE中,(2b)2+a2=($\frac{{b}^{2}}{a}$+a)2,
∴2a2=b2,
在Rt△PCE中.PA=PC=$\sqrt{P{E}^{2}+C{E}^{2}}$=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{3}$a
∴sin∠5=$\frac{PD}{PA}$=$\frac{a}{\sqrt{3}a}$=$\frac{\sqrt{3}}{3}$,
∵AB∥CD,
∴∠BDC=∠3,
∵∠3=∠5,
∴sin∠BDC=$\frac{\sqrt{3}}{3}$.
点评 本题考查了切线性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

| A. | 用表格可以表示任意两个变量之间的关系 | |
| B. | 用关系式可以表示任意两个变量之间的关系 | |
| C. | 用图象可以表示任意两个变量之间的关系 | |
| D. | 在某一变化过程中,数值始终不变的量叫常量 |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
| A. | 3 | B. | 4 | C. | 5 | D. | 8. |
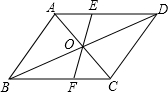 如图,过平行四边形ABCD对角线交点O的直线交AD于E,交BC于F,若AB=4,BC=6,OE=2,那么四边形EFCD周长是( )
如图,过平行四边形ABCD对角线交点O的直线交AD于E,交BC于F,若AB=4,BC=6,OE=2,那么四边形EFCD周长是( )