题目内容
19.计算:$(\frac{1}{3})^{-1}$-$(\sqrt{3}-2)^{0}$+4cos45°-$\sqrt{8}$.分析 直接利用绝对值的性质以及负整数指数幂的性质和特殊角的三角函数值化简求出答案.
解答 解:$(\frac{1}{3})^{-1}$-$(\sqrt{3}-2)^{0}$+4cos45°-$\sqrt{8}$
=3-1+4×$\frac{\sqrt{2}}{2}$-2$\sqrt{2}$
=2.
点评 此题主要考查了实数运算,正确化简各数是解题关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
9.函数y=$\sqrt{x-2}$+1中,自变量x的取值范围是( )
| A. | x>2 | B. | x<2 | C. | x≥2 | D. | x≤2 |
14.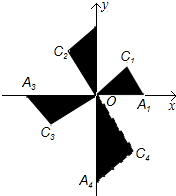 在平面直角坐标系xOy中,Rt△OA1C1、Rt△OA2C2、Rt△OA3C3、Rt△OA4C4…斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3…=30°,若点A1的坐标(3,0),OA1=OC2,OA2=OC3,OA3=OC4…则依此规律OA2016的长为( )
在平面直角坐标系xOy中,Rt△OA1C1、Rt△OA2C2、Rt△OA3C3、Rt△OA4C4…斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3…=30°,若点A1的坐标(3,0),OA1=OC2,OA2=OC3,OA3=OC4…则依此规律OA2016的长为( )
 在平面直角坐标系xOy中,Rt△OA1C1、Rt△OA2C2、Rt△OA3C3、Rt△OA4C4…斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3…=30°,若点A1的坐标(3,0),OA1=OC2,OA2=OC3,OA3=OC4…则依此规律OA2016的长为( )
在平面直角坐标系xOy中,Rt△OA1C1、Rt△OA2C2、Rt△OA3C3、Rt△OA4C4…斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3…=30°,若点A1的坐标(3,0),OA1=OC2,OA2=OC3,OA3=OC4…则依此规律OA2016的长为( )| A. | 3×($\frac{3}{2}$$\sqrt{3}$)2013 | B. | 3×($\frac{3}{2}\sqrt{3}$)2014 | C. | 3×($\frac{3\sqrt{3}}{2}$)2015 | D. | 3×($\frac{3\sqrt{3}}{2}$)2016 |
4.下列说法中正确的有( )
①位似图形都相似;
②两个等腰三角形一定相似;
③两个相似多边形的面积比为4:9,则周长的比为16:81;
④若一个三角形的三边分别比另一个三角形的三边长2cm,那么这两个三角形一定相似.
①位似图形都相似;
②两个等腰三角形一定相似;
③两个相似多边形的面积比为4:9,则周长的比为16:81;
④若一个三角形的三边分别比另一个三角形的三边长2cm,那么这两个三角形一定相似.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.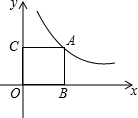 如图,点A是反比例函数y=$\frac{k}{x}(x>0)$图象上一点,AB垂直于x轴,垂足为点B,AC垂直于y轴,垂足为点C,若矩形ABOC的面积为5,则k的值为( )
如图,点A是反比例函数y=$\frac{k}{x}(x>0)$图象上一点,AB垂直于x轴,垂足为点B,AC垂直于y轴,垂足为点C,若矩形ABOC的面积为5,则k的值为( )
 如图,点A是反比例函数y=$\frac{k}{x}(x>0)$图象上一点,AB垂直于x轴,垂足为点B,AC垂直于y轴,垂足为点C,若矩形ABOC的面积为5,则k的值为( )
如图,点A是反比例函数y=$\frac{k}{x}(x>0)$图象上一点,AB垂直于x轴,垂足为点B,AC垂直于y轴,垂足为点C,若矩形ABOC的面积为5,则k的值为( )| A. | 5 | B. | 2.5 | C. | $\sqrt{5}$ | D. | 10 |
9.下列运算正确的是( )
| A. | a2•a4=a8 | B. | 2a+3a=5a | C. | (x-2)2=x2-4 | D. | (x-2)(x+3)=x2-6 |
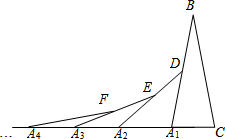 如图,在第1个△A1BC中,∠B=20°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第5个等腰三角形的底角度数是5°.
如图,在第1个△A1BC中,∠B=20°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第5个等腰三角形的底角度数是5°.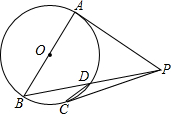 如图,AB是⊙O的直径,PA,PC是⊙O的切线,A,C是切点,PB交⊙O于点D.
如图,AB是⊙O的直径,PA,PC是⊙O的切线,A,C是切点,PB交⊙O于点D.