题目内容
1.在△ABC中,AB=4,BC=6,AC=8,D、E分别是AB、BC的中点,则DE=4.分析 根据三角形的中位线定理得到DE=$\frac{1}{2}$AC,即可得到答案.
解答 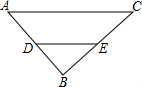 解:如图,∵D、E分别是AB、BC的中点,
解:如图,∵D、E分别是AB、BC的中点,
∴DE是△ABC的中位线,
∴DE=$\frac{1}{2}$AC,
又∵AC=8,
∴DE=4.
故答案是:4.
点评 本题主要考查对三角形的中位线定理的理解和掌握,能正确运用三角形的中位线定理进行计算是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.在解方程$\frac{x-1}{2}$-$\frac{2x+1}{3}$=1时,去分母正确的是( )
| A. | 3(x-1)-2(2x+3)=6 | B. | 3x-3-4x+3=1 | C. | 3(x-1)-2(2x+3)=1 | D. | 3x-3-4x-2=6 |
12.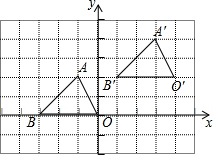 如图,△A′B′O′是由△ABO平移得到的,点A的坐标为(-1,2),它的对应点A′的坐标为(3,4),△ABO内仼意点P(a,b)平移后的对应点P′的坐标为( )
如图,△A′B′O′是由△ABO平移得到的,点A的坐标为(-1,2),它的对应点A′的坐标为(3,4),△ABO内仼意点P(a,b)平移后的对应点P′的坐标为( )
 如图,△A′B′O′是由△ABO平移得到的,点A的坐标为(-1,2),它的对应点A′的坐标为(3,4),△ABO内仼意点P(a,b)平移后的对应点P′的坐标为( )
如图,△A′B′O′是由△ABO平移得到的,点A的坐标为(-1,2),它的对应点A′的坐标为(3,4),△ABO内仼意点P(a,b)平移后的对应点P′的坐标为( )| A. | (a,b) | B. | (-a,-b) | C. | (a+2,b+4) | D. | (a+4,b+2) |
9.函数y=$\sqrt{x-2}$+1中,自变量x的取值范围是( )
| A. | x>2 | B. | x<2 | C. | x≥2 | D. | x≤2 |
6.若用代入法解方程组$\left\{\begin{array}{l}{2x=3y}\\{3x=2y+1}\end{array}\right.$,以下各式代入正确的是( )
| A. | 3x=2($\frac{2}{3}$x)+1 | B. | 3x=2($\frac{2}{3}$y)+1 | C. | 3x=2($\frac{3}{2}$x)+1 | D. | 3x=2x•6x+1 |
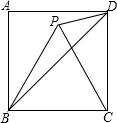 如图,四边形ABCD为正方形,△BPC为等边三角形,连接PD、BD,则∠BDP=30°.
如图,四边形ABCD为正方形,△BPC为等边三角形,连接PD、BD,则∠BDP=30°.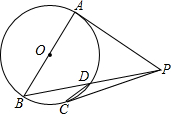 如图,AB是⊙O的直径,PA,PC是⊙O的切线,A,C是切点,PB交⊙O于点D.
如图,AB是⊙O的直径,PA,PC是⊙O的切线,A,C是切点,PB交⊙O于点D.