题目内容
20.解方程式:$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=26①}\\{{x}^{2}-4xy-5{y}^{2}=0②}\end{array}\right.$.分析 将方程②左边因式分解后可得x=-y或x=5y,分别将x=-y、x=5y代入方程①,求每个方程组的解可得.
解答 解:由②可得,(x+y)(x-5y)=0,
即x+y=0或x-5y=0,
∴x=-y或x=5y,
当x=-y时,把x=-y代入①,得:2y2=26,
解得:y=±$\sqrt{13}$,
故方程组的解为:$\left\{\begin{array}{l}{x=-\sqrt{13}}\\{y=\sqrt{13}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\sqrt{13}}\\{y=-\sqrt{13}}\end{array}\right.$;
当x=5y时,把x=5y代入①,得:25y2+y2=26,
解得:y=±1,
故方程组的解为:$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-5}\\{y=-1}\end{array}\right.$,;
综上,该方程组的解为:$\left\{\begin{array}{l}{x=-\sqrt{13}}\\{y=\sqrt{13}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\sqrt{13}}\\{y=-\sqrt{13}}\end{array}\right.$或$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-5}\\{y=-1}\end{array}\right.$.
点评 本题主要考查解高次方程的能力,解高次方程的根本思想是化归思想,次数较高可通过因式分解再代入等方法降幂求解即可.

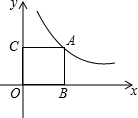 如图,点A是反比例函数y=$\frac{k}{x}(x>0)$图象上一点,AB垂直于x轴,垂足为点B,AC垂直于y轴,垂足为点C,若矩形ABOC的面积为5,则k的值为( )
如图,点A是反比例函数y=$\frac{k}{x}(x>0)$图象上一点,AB垂直于x轴,垂足为点B,AC垂直于y轴,垂足为点C,若矩形ABOC的面积为5,则k的值为( )| A. | 5 | B. | 2.5 | C. | $\sqrt{5}$ | D. | 10 |
| A. | 2-1 | B. | -1-2 | C. | -(2-1) | D. | -(1+2) |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | a2•a4=a8 | B. | 2a+3a=5a | C. | (x-2)2=x2-4 | D. | (x-2)(x+3)=x2-6 |
| A. | 5 | B. | 10 | C. | 36 | D. | 72 |
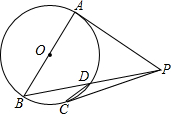 如图,AB是⊙O的直径,PA,PC是⊙O的切线,A,C是切点,PB交⊙O于点D.
如图,AB是⊙O的直径,PA,PC是⊙O的切线,A,C是切点,PB交⊙O于点D.