题目内容
18.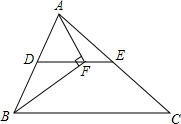 如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( )
如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据直角三角形斜边上中线是斜边的一半可得DF=$\frac{1}{2}$AB=AD=BD=5且∠ABF=∠BFD,结合角平分线可得∠CBF=∠DFB,即DE∥BC,进而可得DE=8,由EF=DE-DF可得答案.
解答 解:∵AF⊥BF,
∴∠AFB=90°,
∵AB=10,D为AB中点,
∴DF=$\frac{1}{2}$AB=AD=BD=5,
∴∠ABF=∠BFD,
又∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠CBF=∠DFB,
∴DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}$=$\frac{AD}{AB}$,即$\frac{DE}{16}=\frac{5}{10}$,
解得:DE=8,
∴EF=DE-DF=3,
故选:B.
点评 本题主要考查直角三角形的性质和相似三角形的判定与性质,熟练运用其判定与性质是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
9.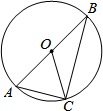 如图,已知⊙O为△ABC的外接圆,且AB为⊙O的直径,若OC=5,AC=6,则BC长为( )
如图,已知⊙O为△ABC的外接圆,且AB为⊙O的直径,若OC=5,AC=6,则BC长为( )
 如图,已知⊙O为△ABC的外接圆,且AB为⊙O的直径,若OC=5,AC=6,则BC长为( )
如图,已知⊙O为△ABC的外接圆,且AB为⊙O的直径,若OC=5,AC=6,则BC长为( )| A. | 10 | B. | 9 | C. | 8 | D. | 无法确定 |
13.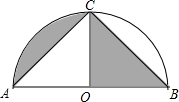 如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=$\sqrt{2}$,则图中阴影部分的面积是( )
如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=$\sqrt{2}$,则图中阴影部分的面积是( )
 如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=$\sqrt{2}$,则图中阴影部分的面积是( )
如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=$\sqrt{2}$,则图中阴影部分的面积是( )| A. | $\frac{π}{4}$ | B. | $\frac{1}{2}$$+\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{1}{2}$+$\frac{π}{2}$ |
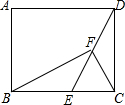 如图,矩形ABCD中,点E为BC上一点,F为DE的中点,且∠BFC=90°.
如图,矩形ABCD中,点E为BC上一点,F为DE的中点,且∠BFC=90°.
 如图,在?ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )
如图,在?ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )