题目内容
8.化简($\sqrt{3}$-2)2015•($\sqrt{3}+2$)2016的结果为-$\sqrt{3}$-2.分析 根据同底数幂的乘法法则和积的乘方法则把原式变形,根据平方差公式计算即可.
解答 解:原式=($\sqrt{3}$-2)2015•($\sqrt{3}+2$)2015•($\sqrt{3}$+2)
=[($\sqrt{3}$-2)•($\sqrt{3}+2$)]2015•($\sqrt{3}$+2)
=-1ו($\sqrt{3}$+2)
=-$\sqrt{3}$-2.
故答案为:-$\sqrt{3}$-2.
点评 本题考查的是二次根式的混合运算,掌握积的乘方法则、灵活运用平方差公式是解题的关键.

练习册系列答案
相关题目
18.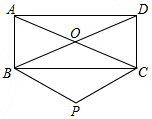 如图,矩形ABCD的对角线相交于点O,PB∥AC,PC∥BD,PB、PC相交于点P.
如图,矩形ABCD的对角线相交于点O,PB∥AC,PC∥BD,PB、PC相交于点P.
(1)猜想四边形PCOB是什么四边形,并说明理由;
(2)当矩形ABCD满足什么条件时,四边形PCOB是正方形.
 如图,矩形ABCD的对角线相交于点O,PB∥AC,PC∥BD,PB、PC相交于点P.
如图,矩形ABCD的对角线相交于点O,PB∥AC,PC∥BD,PB、PC相交于点P.(1)猜想四边形PCOB是什么四边形,并说明理由;
(2)当矩形ABCD满足什么条件时,四边形PCOB是正方形.
3.对于两个不相等的示数a,b,我们规定符号Max{a,b}表示a、b中的较大值,如:Max{2,4}=4,按照这个规定,方程Max{x,-x}=$\frac{2x+1}{x}$的解为( )
| A. | 1+$\sqrt{2}$或-1 | B. | 2-$\sqrt{2}$ | C. | 1+$\sqrt{2}$或1-$\sqrt{2}$ | D. | 1-$\sqrt{2}$或-1 |
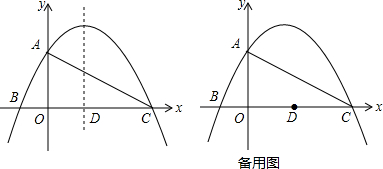
 某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据计算CD的长为22cm(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据计算CD的长为22cm(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
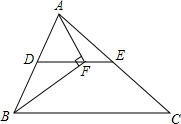 如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( )
如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( )