题目内容
8.把抛物线y=x2先向右平移2个单位,再向上平移3个单位,平移后抛物线的表达式是y=(x-2)2+3.分析 先确定y=x2的顶点坐标为(0,0),再根据点平移的规律得到点(0,0)平移后对应点的坐标,然后根据顶点式写出平移后抛物线的表达式.
解答 解:抛物线y=x2的顶点坐标为(0,0),点(0,0)向右平移2个单位,再向上平移3个单位所得对应点的坐标为(2,3),所以平移后抛物线的表达式为y=(x-2)2+3.
故答案为y=(x-2)2+3.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
16.方程$\frac{2x+1}{x-1}$=3的解是( )
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | -4 | D. | 4 |
3.已知一个正多边形的内角是140°,则这个正多边形的边数是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
13.科学家在实验中检测出某微生物约为0.0000035米,将0.0000035用科学记数法表示为( )
| A. | 3.5×10-6 | B. | 3.5×106 | C. | 3.5×10-5 | D. | 35×10-5 |
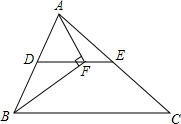 如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( )
如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( ) “万人马拉松”活动组委会计划制作运动衫分发给参与者,为此,调查了部分参与者,以决定制作橙色、黄色、白色、红色四种颜色运动衫的数量.根据得到的调查数据,绘制成如图所示的扇形统计图.若本次活动共有12000名参与者,则估计其中选择红色运动衫的约有2400名.
“万人马拉松”活动组委会计划制作运动衫分发给参与者,为此,调查了部分参与者,以决定制作橙色、黄色、白色、红色四种颜色运动衫的数量.根据得到的调查数据,绘制成如图所示的扇形统计图.若本次活动共有12000名参与者,则估计其中选择红色运动衫的约有2400名.