题目内容
2.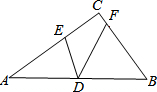 如图,在△ABC中,∠ACB=90°,D为边AB的中点,E,F分别为边AC,BC上的点,且AE=AD,BF=BD.若DE=2$\sqrt{2}$,DF=4,则AB的长为4$\sqrt{5}$.
如图,在△ABC中,∠ACB=90°,D为边AB的中点,E,F分别为边AC,BC上的点,且AE=AD,BF=BD.若DE=2$\sqrt{2}$,DF=4,则AB的长为4$\sqrt{5}$.
分析 延长FD到M使得DM=DF,连接AM、EM、EF,作EN⊥DF于N,先证明∠EDF=45°,在RT△EMN中求出EM,再证明△AEM是等腰直角三角形即可解决问题.
解答 解:如图,延长FD到M使得DM=DF,连接AM、EM、EF,作EN⊥DF于N.
∵∠C=90°,
∴∠BAC+∠B=90°,
∵AE=AD,BF=BD,
∴∠AED=∠ADE,∠BDF=∠BFD,
∴2∠ADE+∠BAC=180°,2∠BDF+∠B=180°,
∴2∠ADE+2∠BDF=270°,
∴∠ADE+∠BDF=135°,
∴∠EDF=180°-(∠ADE+∠BDF)=45°,
∵∠END=90°,DE=2$\sqrt{2}$,
∴∠EDN=∠DEN=45°,
∴EN=DN=2,
在△DAM和△DBF中,
$\left\{\begin{array}{l}{DA=DB}\\{∠ADM=∠BDF}\\{DM=DF}\end{array}\right.$,
∴△ADM≌△BDF,
∴BF=AM=BD=AD=AE,∠MAD=∠B,
∴∠MAE=∠MAD+∠BAC=90°,
∴EM=$\sqrt{2}$AM,
在RT△EMN中,∵EN=2,MN=DM+DN=6,
∴EM=$\sqrt{E{N}^{2}+M{N}^{2}}$=2$\sqrt{10}$,
∴AM=2$\sqrt{5}$,AB=2AM=4$\sqrt{5}$.
故答案为4$\sqrt{5}$.
点评 本题考查全等三角形的判定和性质、勾股定理、等腰直角三角形的判定和性质,解题的突破口是添加辅助线构造RT△EMF以及倍长中线构造全等三角形,题目有点难度.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
10.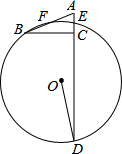 如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
 如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )| A. | 13 | B. | $2\sqrt{26}$ | C. | $3\sqrt{26}$ | D. | $\frac{27}{2}$ |
14. 如图,AD⊥BC,ED⊥AB,表示点A到直线DE距离的是( )
如图,AD⊥BC,ED⊥AB,表示点A到直线DE距离的是( )
 如图,AD⊥BC,ED⊥AB,表示点A到直线DE距离的是( )
如图,AD⊥BC,ED⊥AB,表示点A到直线DE距离的是( )| A. | 线段AD的长度 | B. | 线段AE的长度 | C. | 线段BE的长度 | D. | 线段DE的长度 |
11.某公司生产的A种产品,每件成本是2元,每件售价是3元,一年的销售量是10万件.为了获得更多的利润,公司准备拿出一定资金来做广告.根据经验,每年投入的广告费为x(万元)时,产品的年销售量是原来的y倍,且y是x的二次函数,公司作了预测,知x与y之间的对应关系如表:
(1)根据表中,求y关于x的函数关系式;
(2)如果把利润看成是销售总额减去成本和广告费,请你写出年利润S(万元)与广告费x(万元)的函数关系式;
(3)根据上面的函数关系式,你认为每年投入多少广告费最合适?为什么?
| x(万元) | 0 | 1 | 2 | … |
| y | 1 | 1.5 | 1.8 | … |
(2)如果把利润看成是销售总额减去成本和广告费,请你写出年利润S(万元)与广告费x(万元)的函数关系式;
(3)根据上面的函数关系式,你认为每年投入多少广告费最合适?为什么?
12. 如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于( )
如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于( )
 如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于( )
如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
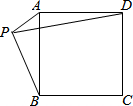 如图,P是正方形ABCD外一点,PA=$\sqrt{2}$,PB=4,则PD长度的最大值为6.
如图,P是正方形ABCD外一点,PA=$\sqrt{2}$,PB=4,则PD长度的最大值为6.