题目内容
9.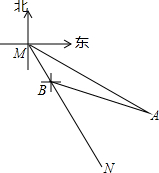 如图,东站枢纽建设要新建一条从M地到N地的公路,测得N点位于M点的南偏东30°,A点位于M点的南偏东60°,以A点为中心,半径为500米的圆形区域为文物保护区,又在B点测得BA的方向为南偏东75°,量得MB=400米,请计算后回答公路是否会穿越文物保护区(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,东站枢纽建设要新建一条从M地到N地的公路,测得N点位于M点的南偏东30°,A点位于M点的南偏东60°,以A点为中心,半径为500米的圆形区域为文物保护区,又在B点测得BA的方向为南偏东75°,量得MB=400米,请计算后回答公路是否会穿越文物保护区(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
分析 过点A作AC⊥BN于C,利用三角函数求出AC的长,与500米进行比较就可以求解.
解答 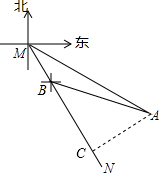 解:过A作AC⊥BN于C,
解:过A作AC⊥BN于C,
由题意得∠CMA=30°,∠CBA=75°-30°=45°,MB=400m,
设AC=xm,
在Rt△AMC中,$\frac{AC}{MC}=tan{30^0}=\frac{{\sqrt{3}}}{3}$,$MC=\sqrt{3}x$,
所以$BC=MC-MB=\sqrt{3}x-400$,
在Rt△ABC中,$\frac{AC}{BC}=1$,
∴$\sqrt{3}x-400=x$,
∴$x=\frac{400}{{\sqrt{3}-1}}=200(\sqrt{3}+1)≈200(1.732+1)=546.4(m)$,
因为AC=546.4m>500m,
所以公路不会穿过文物保护区.
点评 考查了解直角三角形的应用-方向角问题,解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
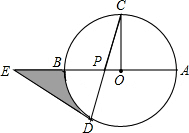 如图,⊙O的半径OC与直径AB垂直,点P在OB上,CP的延长线交⊙O于点D,在OB的延长线上取点E,使ED=EP.
如图,⊙O的半径OC与直径AB垂直,点P在OB上,CP的延长线交⊙O于点D,在OB的延长线上取点E,使ED=EP.