题目内容
2．已知三角形三边长分别是1、x、2，且x为整数，那么x的值是2．分析 根据三角形的三边关系：两边之和大于第三边，两边之差小于第三边，求解即可．
解答 解：∵三角形的三边长分别为1，x，2，
∴第三边的取值范围为：1＜x＜3
∵x为整数，
∴x=2．
故答案为：2．
点评 考查了三角形的三边关系，此类求范围的问题，实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可，确定x的值．
练习册系列答案
初中学业考试导与练系列答案
相关题目
12．
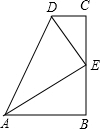在数学活动课上，小明提出这样一个问题：∠B=∠C=90°，E是BC的中点，DE平分∠ADC，如图，则下列说法正确的有（ ）个．
（1）AE平分∠DAB；（2）△EBA≌△DCE；（3）AB+CD=AD；（4）AE⊥DE；（5）AB∥CD．
在数学活动课上，小明提出这样一个问题：∠B=∠C=90°，E是BC的中点，DE平分∠ADC，如图，则下列说法正确的有（ ）个．（1）AE平分∠DAB；（2）△EBA≌△DCE；（3）AB+CD=AD；（4）AE⊥DE；（5）AB∥CD．
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
10．
如图，在△ABC中，点D在线段BC上且∠BAD=∠C，BD=2，CD=6，则AB的值是（ ）
如图，在△ABC中，点D在线段BC上且∠BAD=∠C，BD=2，CD=6，则AB的值是（ ）| A． | 12 | B． | 8 | C． | 4 | D． | 3 |
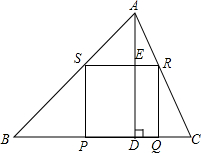如图，AD是△ABC的高，点P，Q在BC边上，点R在AC边上，点S在AB边上，BC=30cm，AD=20cm，四边形PQRS是正方形．
如图，在△ABC中，AB=AC，点E在CA延长线上，EP⊥BC于点P，交AB于点F．
12．一次函数y=-2x-4的图象与y轴的交点坐标为（ ）
| A． | （-4，0） | B． | （-2，0） | C． | （0，-4） | D． | （0，-2） |