题目内容
5．小刚想测量教学楼的高度，他用一根绳子从楼顶垂下，发现绳子垂到地面后还多了2米，当他把绳子的下端拉开6米后，发现绳子下端刚好接触地面，则教学楼的高度是（ ）米．| A． | 10 | B． | 12 | C． | 14 | D． | 8 |
分析 根据题意列出已知条件再根据勾股定理求得旗杆的高度．
解答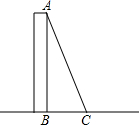 
解：已知AB为旗杆的高度，AC=AB+2，BC=6米，求AB的高度．
因为AB⊥BC，根据勾股定理得AB2=AC2-BC2，
则得AB2=（AB+2）2-62，
解得：AB=8，
所以旗杆高度为8米．
故选：D．
点评 此题主要考查了勾股定理的应用，正确表示出三角形各边长是解题关键．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
15．
如图，表示抛物线y=ax2+bx+c的一部分图象，它与x轴的一个交点为A，与y轴交于B，则b的取值范围是（ ）
如图，表示抛物线y=ax2+bx+c的一部分图象，它与x轴的一个交点为A，与y轴交于B，则b的取值范围是（ ）| A． | -2＜b＜0 | B． | -1＜b＜0 | C． | -$\frac{1}{2}$＜b＜0 | D． | 0＜b＜0 |
如图，已知点P在AB上，∠APD=∠APC，∠DBA=∠CBA，求证：AC=AD．
如图，已知∠EFD=∠BCA，BC=EF，AF=DC，则AB=DE．请通过完成以下填空的形式说明理由．
10．在一次实验中，测得两个变量x与y之间的对应值如下表所示：
（1）根据表中数据，请探究y与x之间的函数关系式；
（2）根据你的关系式，求出当y=-15时x的值；
（3）当x从-10连续变化到15时，指出y的变化规律并求出y的最大值和最小值？
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | -5 | -3 | -1 | 1 | 3 | 5 | 7 | … |
（2）根据你的关系式，求出当y=-15时x的值；
（3）当x从-10连续变化到15时，指出y的变化规律并求出y的最大值和最小值？
17．下列说法错误的是（ ）
| A． | 单项式x的系数和次数都是1 | |
| B． | $\frac{1}{2}$不是单项式 | |
| C． | 多项式3x2y+2xy-3x+y中一次项的系数分别是-3，1 | |
| D． | -$\frac{2xy}{3}$是系数为-$\frac{2}{3}$的二次单项式 |
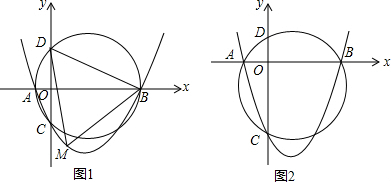
如图，在△ABC中，D为三角形内一点，∠A=35°，∠ABD=20°，∠ACD=25°，BD∥CE，则∠DCE=75°．