题目内容
6.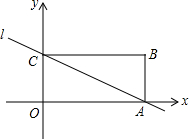 矩形ABCD在平面直角坐标系中,且顶点O为坐标原点,已知点B(3,2),则对角线AC所在的直线l对应的解析式为y=-$\frac{2}{3}$x+2.
矩形ABCD在平面直角坐标系中,且顶点O为坐标原点,已知点B(3,2),则对角线AC所在的直线l对应的解析式为y=-$\frac{2}{3}$x+2.
分析 由四边形ABCO为矩形,利用矩形的性质得到对边平行且相等,根据B的坐标确定出OA与OC的长,进而求出A与C的坐标,设直线AC解析式为y=kx+b,把A与C坐标代入求出k与b的值,即可确定出直线AC解析式.
解答 解:∵四边形ABCO为矩形,
∴BC∥x轴,AB∥y轴,
∵B(3,2),
∴OA=BC=3,AB=OC=2,
∴A(3,0),C(0,2),
设直线AC解析式为y=kx+b,
把A与C坐标代入得:$\left\{\begin{array}{l}{3k+b=0}\\{b=2}\end{array}\right.$,
解得:k=-$\frac{2}{3}$,b=2,
则直线AC解析式为y=-$\frac{2}{3}$x+2.
点评 此题考查了待定系数法求一次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
17.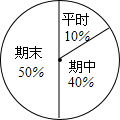 小军八年级上学期的数学成绩如表所示:易知小军上学期平时的平均成绩105分.
小军八年级上学期的数学成绩如表所示:易知小军上学期平时的平均成绩105分.
如果学期总评成绩按扇形图所示的权重计算,小军上学期的总评成绩是109.7分.
 小军八年级上学期的数学成绩如表所示:易知小军上学期平时的平均成绩105分.
小军八年级上学期的数学成绩如表所示:易知小军上学期平时的平均成绩105分.| 测验类别 | 平时 | 期中考试 | 期末考试 | |||
| 测验1 | 测验2 | 测验3 | 测验4 | |||
| 成绩 | 110 | 105 | 95 | 110 | 108 | 112 |
1.已知一次函数y=(1-2k)x+k的图象经过第一、二、三象限,则k的取值范围是( )
| A. | k>0 | B. | k<0 | C. | 0<k<$\frac{1}{2}$ | D. | k<$\frac{1}{2}$ |
15.已知△ABC∽△DEF,且相似比为2:3,则△ABC与△DEF的对应高之比为( )
| A. | 2:3 | B. | 3:2 | C. | 4:9 | D. | 9:4 |