题目内容
若关于x的一元二次方程kx2+4x+3=0有实数根,则k的取值范围是 .
考点:根的判别式,一元二次方程的定义
专题:
分析:根据方程根的情况可以判定其根的判别式的取值范围,进而可以得到关于k的不等式,解得即可,同时还应注意二次项系数不能为0.
解答:解:∵关于x的一元二次方程kx2+4x+3=0有实数根,
∴△=b2-4ac=16-12k≥0,k≠0,
解得:k≤
,
则k的取值范围是k≤
且k≠0;
故答案为:k≤
且k≠0.
∴△=b2-4ac=16-12k≥0,k≠0,
解得:k≤
| 4 |
| 3 |
则k的取值范围是k≤
| 4 |
| 3 |
故答案为:k≤
| 4 |
| 3 |
点评:本题考查了根的判别式,解题的关键是了解根的判别式如何决定一元二次方程根的情况.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
下列说法中,正确的是( )
A、单项式
| ||||
| B、-3x2y+4x-1是三次三项式,常数项是1 | ||||
| C、单项式a的系数是0,次数是0 | ||||
D、单项式-
|
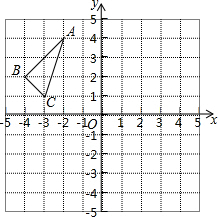 △ABC在平面直角坐标系中的位置如图,其中每个小正方形的边长为1个单位长度.
△ABC在平面直角坐标系中的位置如图,其中每个小正方形的边长为1个单位长度.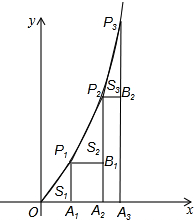 如图,已知A1,A2,A3…,A2008是x轴上的点,且OA1=A1A2=A2A3=…=A2007A2008=1,分别过点A1,A2,A3,…A2008作x轴的垂线交二次函数y=x2(x>0)的图象于点P1,P2,P3…,P2008点,若记△OA1P1的面积S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△P2007B2007P2008的面积为S2008,则S2008-S2007=
如图,已知A1,A2,A3…,A2008是x轴上的点,且OA1=A1A2=A2A3=…=A2007A2008=1,分别过点A1,A2,A3,…A2008作x轴的垂线交二次函数y=x2(x>0)的图象于点P1,P2,P3…,P2008点,若记△OA1P1的面积S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△P2007B2007P2008的面积为S2008,则S2008-S2007=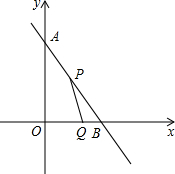 如图,直线y=-
如图,直线y=-