题目内容
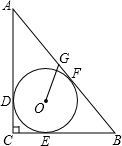 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,⊙O为△ABC内切圆,与三边分别相切于D、E、F.
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,⊙O为△ABC内切圆,与三边分别相切于D、E、F.(1)求⊙O半径;
(2)若G为AB中点,求线段OG长度.
考点:三角形的内切圆与内心
专题:计算题
分析:(1)连接OD、OE、OF,如图,设⊙O半径为r,在Rt△ABC中根据勾股定理计算出AB=10,再证明四边形ODCE为正方形,则CD=CE=r,AD=8-r,BE=6-r,
根据切线长定理得AF=AD=8-r,BF=BE=6-r,所以8-r+6-r=10,解方程即可得到r的值;
(2)由=
AB=5,BF=4得到GF=BG-BF=1,然后在Rt△OGF中根据勾股定理可计算出OG.
根据切线长定理得AF=AD=8-r,BF=BE=6-r,所以8-r+6-r=10,解方程即可得到r的值;
(2)由=
| 1 |
| 2 |
解答:解:(1)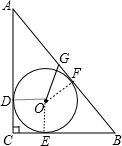 连接OD、OE、OF,如图,设⊙O半径为r,
连接OD、OE、OF,如图,设⊙O半径为r,
在Rt△ABC中,∵AC=8,BC=6,
∴AB=
=10,
∵⊙O为△ABC内切圆,与三边分别相切于D、E、F,
∴OD⊥AC,OE⊥BC,OF⊥AB,
∴四边形ODCE为矩形,
∵OD=OE,
∴四边形ODCE为正方形,
∴CD=CE=r,
∴AD=8-r,BE=6-r,
∵AF=AD=8-r,BF=BE=6-r,
∴8-r+6-r=10,
∴r=2,
即⊙O半径为2;
(2)∵G为AB中点,
∴BG=
AB=5,
而BF=6-r=4,
∴GF=BG-BF=5-4=1,
在Rt△OGF中,∵OF=2,GF=1,
∴OG=
=
.
 连接OD、OE、OF,如图,设⊙O半径为r,
连接OD、OE、OF,如图,设⊙O半径为r,在Rt△ABC中,∵AC=8,BC=6,
∴AB=
| BC2+AC2 |
∵⊙O为△ABC内切圆,与三边分别相切于D、E、F,
∴OD⊥AC,OE⊥BC,OF⊥AB,
∴四边形ODCE为矩形,
∵OD=OE,
∴四边形ODCE为正方形,
∴CD=CE=r,
∴AD=8-r,BE=6-r,
∵AF=AD=8-r,BF=BE=6-r,
∴8-r+6-r=10,
∴r=2,
即⊙O半径为2;
(2)∵G为AB中点,
∴BG=
| 1 |
| 2 |
而BF=6-r=4,
∴GF=BG-BF=5-4=1,
在Rt△OGF中,∵OF=2,GF=1,
∴OG=
| OF2+GF2 |
| 5 |
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了切线的性质与切线长定理.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 a,b两数在数轴上的位置如图所示,下列结论中正确的是( )
a,b两数在数轴上的位置如图所示,下列结论中正确的是( )| A、a<0,b>0 |
| B、a+b<0 |
| C、ab>0 |
| D、a-b<0 |
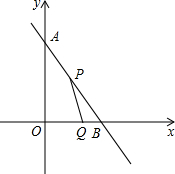 如图,直线y=-
如图,直线y=- 如图,AB是⊙O的直径,AB=10,圆心角∠AOC=60°,点D是
如图,AB是⊙O的直径,AB=10,圆心角∠AOC=60°,点D是
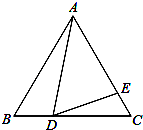 如图,在边长为9的等边△ABC中,BD=3,∠ADE=60°,求AE的长.
如图,在边长为9的等边△ABC中,BD=3,∠ADE=60°,求AE的长.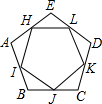 如图,H、I、J、K、L分别是正五边形ABCDE各边的中点,求证:五边形HIJKL是正五边形.
如图,H、I、J、K、L分别是正五边形ABCDE各边的中点,求证:五边形HIJKL是正五边形.