题目内容
6.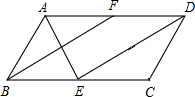 如图,已知平行四边形ABCD中,∠ABC=60°,BC=2AB,点E、F分别是BC、AD的中点,连接AE、DE、BF.
如图,已知平行四边形ABCD中,∠ABC=60°,BC=2AB,点E、F分别是BC、AD的中点,连接AE、DE、BF.(1)求证:AE=CD;
(2)若BF=6,求DE的长.
分析 (1)由四边形ABCD是平行四边形,可得AB=CD,又由∠ABC=60°,BC=2AB,点E、F分别是BC、AD的中点,可得△ABE是等边三角形,继而证得结论;
(2)由平行四边形ABCD中,点E、F分别是BC、AD的中点,易证得四边形BFDE是平行四边形,继而求得答案.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,
∵BC=2AB,点E是BC的中点,
∴AB=BE,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴AB=AE,
∴AE=CD;
(2)解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵点E、F分别是BC、AD的中点,
∴BE=DF,
∴四边形BFDE是平行四边形,
∴DE=BF=6.
点评 此题考查了平行四边形的判定与性质以及等边三角形的判定与性质.注意证得△ABE是等边三角形与四边形BFDE是平行四边形是解此题的关键.

练习册系列答案
相关题目
17.某校准备组建七年级男生篮球队,有60名男生报名,体育老师对60名男生的身高进行了测量,获得60个数据,数学老师将这些数据分成5组绘制成绩分布直方图,已知从左至右的5个小长方形的高度比为1:3:5:4:2,则第五个小组的频数为( )
| A. | 12 | B. | 16 | C. | 20 | D. | 8 |
1.若x2-kx+9是一个完全平方式,则k的值为( )
| A. | -3 | B. | -6 | C. | ±3 | D. | ±6 |
15.下面的调查中,不适合抽样调查的是( )
| A. | 一批炮弹的杀伤力的情况 | B. | 了解一批灯泡的使用寿命 | ||
| C. | 全面人口普查 | D. | 全市学生每天参加体育锻炼的时间 |
 如图,∠1+∠2=230°,b∥c,则∠1、∠2、∠3、∠4各是多少度?
如图,∠1+∠2=230°,b∥c,则∠1、∠2、∠3、∠4各是多少度? 如图,点P是等边三角形ABC内的一点,连结PB、PC.将△PBC绕点B逆时针旋转到△P′BA的位置,则∠PBP′的度数是60°.
如图,点P是等边三角形ABC内的一点,连结PB、PC.将△PBC绕点B逆时针旋转到△P′BA的位置,则∠PBP′的度数是60°.