题目内容
14.在各个内角都相等的多边形中,一个外角等于一个内角的$\frac{1}{4}$,求这个多边形每一个内角的度数和它的边数.分析 已知关系为:一个外角=一个内角×$\frac{1}{4}$,隐含关系为:一个外角+一个内角=180°,由此即可解决问题.
解答 解:设该多边形为n边形
∵多边形一个外角等于一个内角的$\frac{1}{4}$
∴多边形的内角和为360°×4=1440°,
∴(n-2)×180°=1440°
∴n-2=8
∴n=10,
∴该多边形每一个内角的度数为(360°÷10)×4=144°,
答:该多边形每一个内角的度数为144°,该多边形为10边形.
点评 本题考查了多边形内角与外角的关系,用到的知识点为:各个内角相等的多边形的边数可利用外角来求,边数=360÷一个外角的度数.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
9. 如图所示,数轴上点A所表示的数为a,则a的值是( )
如图所示,数轴上点A所表示的数为a,则a的值是( )
 如图所示,数轴上点A所表示的数为a,则a的值是( )
如图所示,数轴上点A所表示的数为a,则a的值是( )| A. | $\sqrt{5}$-1 | B. | -$\sqrt{5}$+1 | C. | $\sqrt{5}$+1 | D. | $\sqrt{5}$ |
3. 如图,能判断a∥b的条件是( )
如图,能判断a∥b的条件是( )
 如图,能判断a∥b的条件是( )
如图,能判断a∥b的条件是( )| A. | ∠1=∠2 | B. | ∠2=∠4 | C. | ∠2+∠4=180° | D. | ∠2+∠3=180° |
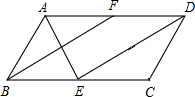 如图,已知平行四边形ABCD中,∠ABC=60°,BC=2AB,点E、F分别是BC、AD的中点,连接AE、DE、BF.
如图,已知平行四边形ABCD中,∠ABC=60°,BC=2AB,点E、F分别是BC、AD的中点,连接AE、DE、BF.