题目内容
11.如果方程组$\left\{\begin{array}{l}{x=4}\\{by+ax=5}\end{array}\right.$的解与方程组$\left\{\begin{array}{l}{y=3}\\{bx+ay=2}\end{array}\right.$的解相同,则a+b的值为1.分析 把$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$代入方程组$\left\{\begin{array}{l}{by+ax=5}\\{bx+ay=2}\end{array}\right.$,得到一个关于a,b的方程组,将方程组的两个方程左右两边分别相加,整理即可得出a+b的值.
解答 解:把$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$代入方程组$\left\{\begin{array}{l}{by+ax=5}\\{bx+ay=2}\end{array}\right.$,
得:$\left\{\begin{array}{l}{3b+4a=5①}\\{4b+3a=2②}\end{array}\right.$,
①+②,得:7(a+b)=7,
则a+b=1.
故答案为1.
点评 此题主要考查了二元一次方程组的解的定义:一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.

练习册系列答案
相关题目
3. 如图,能判断a∥b的条件是( )
如图,能判断a∥b的条件是( )
 如图,能判断a∥b的条件是( )
如图,能判断a∥b的条件是( )| A. | ∠1=∠2 | B. | ∠2=∠4 | C. | ∠2+∠4=180° | D. | ∠2+∠3=180° |
1.下列计算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | $\sqrt{5}$-$\sqrt{4}$=1 | C. | $\sqrt{(3-π)^{2}}$=3-π | D. | $\root{3}{{2}^{3}}$=2 |
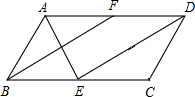 如图,已知平行四边形ABCD中,∠ABC=60°,BC=2AB,点E、F分别是BC、AD的中点,连接AE、DE、BF.
如图,已知平行四边形ABCD中,∠ABC=60°,BC=2AB,点E、F分别是BC、AD的中点,连接AE、DE、BF. 如图,a∥b,若∠2=130°,则∠1=50°.
如图,a∥b,若∠2=130°,则∠1=50°.