题目内容
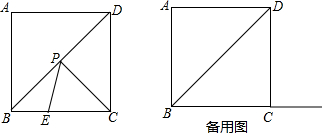
16. 如图,点P是等边三角形ABC内的一点,连结PB、PC.将△PBC绕点B逆时针旋转到△P′BA的位置,则∠PBP′的度数是60°.
如图,点P是等边三角形ABC内的一点,连结PB、PC.将△PBC绕点B逆时针旋转到△P′BA的位置,则∠PBP′的度数是60°.
分析 首先根据等边三角形的性质可得∠ABC=60°,然后再根据旋转可得∠ABP′=∠CBP,进而可得∠PBP′的度数.
解答 解:∵△ABC是等边三角形,
∴∠ABC=60°,
∵△PBC绕点B逆时针旋转到△P′BA的位置,
∴∠ABP′=∠CBP,
∴∠PBP′=∠ABP′+∠ABP=∠PBC+∠ABP=60°,
故答案为:60°.
点评 此题主要考查了等边三角形的性质和旋转的性质,关键是掌握旋转前、后的图形全等.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
7.甲班有54人,乙班有48人,要使甲班人数是乙班人数的2倍,设从乙班调往甲班x人,可列方程( )
| A. | 54+x=2(48-x) | B. | 48+x=2(54-x) | C. | 54-x=2×48 | D. | 48+x=2×54 |
1.下列计算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | $\sqrt{5}$-$\sqrt{4}$=1 | C. | $\sqrt{(3-π)^{2}}$=3-π | D. | $\root{3}{{2}^{3}}$=2 |
8.如果一个三角形的两边长分别是1cm,2cm,那么这个三角形第三边长可能是( )
| A. | 1cm | B. | 2.5cm | C. | 3cm | D. | 4cm |
8.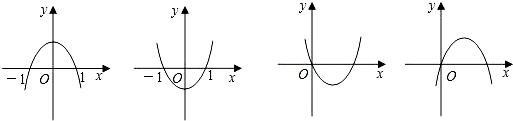 设a、b为常数,且b>0,抛物线y=ax2+bx+a2-5a-6为下列图形之一,则a的值为( )
设a、b为常数,且b>0,抛物线y=ax2+bx+a2-5a-6为下列图形之一,则a的值为( )
 设a、b为常数,且b>0,抛物线y=ax2+bx+a2-5a-6为下列图形之一,则a的值为( )
设a、b为常数,且b>0,抛物线y=ax2+bx+a2-5a-6为下列图形之一,则a的值为( )| A. | 6或-1 | B. | -6或 1 | C. | 6 | D. | -1 |
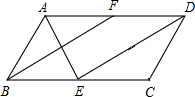 如图,已知平行四边形ABCD中,∠ABC=60°,BC=2AB,点E、F分别是BC、AD的中点,连接AE、DE、BF.
如图,已知平行四边形ABCD中,∠ABC=60°,BC=2AB,点E、F分别是BC、AD的中点,连接AE、DE、BF.