题目内容
19. 如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
分析 当四边形EDD′F为菱形时,△A′DE是等腰三角形,△A′DE≌△EFC′.先证明CD=DA=DB,得到∠DAC=∠DCA,由AC∥A′C′即可得到∠DA′E=∠DEA′由此即可判断△DA′E的形状.由EF∥AB推出∠CEF=∠EA′D,∠EFC=∠A′D′C=∠A′DE,再根据A′D=DE=EF即可证明.
解答  解:当四边形EDD′F为菱形时,△A′DE是等腰三角形,△A′DE≌△EFC′.
解:当四边形EDD′F为菱形时,△A′DE是等腰三角形,△A′DE≌△EFC′.
理由:∵△BCA是直角三角形,∠ACB=90°,AD=DB,
∴CD=DA=DB,
∴∠DAC=∠DCA,
∵A′C′∥AC,
∴∠DA′E=∠A,∠DEA′=∠DCA,
∴∠DA′E=∠DEA′,
∴DA′=DE,
∴△A′DE是等腰三角形.
∵四边形DEFD′是菱形,
∴EF=DE=DA′,EF∥DD′,
∴∠C′EF=∠DA′E,∠EFC′=∠C′D′A′,
∵CD∥C′D′,
∴∠A′DE=∠A′D′C′=∠EFC′,
在△A′DE和△EFC′中,
$\left\{\begin{array}{l}{∠EA′D=∠C′EF}\\{A′D=EF}\\{∠A′DE=∠EFC′}\end{array}\right.$,
∴△A′DE≌△EFC′.
点评 本题考查平移、菱形的性质、全等三角形的判定和性质、直角三角形斜边中线定理等知识,解题的关键是灵活运用这些知识解决问题,属于中考常考题型.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
14. 如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )
如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )
 如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )
如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )| A. | 100° | B. | 72° | C. | 64° | D. | 36° |
11.已知在△ABC中,AB=AC,AD是角平分线,点D在边BC上,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AC}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )
| A. | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ | C. | -$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ |
9.下列计算正确的是( )
| A. | (xy)3=xy3 | B. | x5÷x5=x | ||
| C. | 3x2•5x3=15x5 | D. | 5x2y3+2x2y3=10x4y9 |
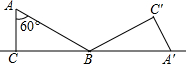 如图,△ABC中,∠C=90°,∠A=60°,AB=2$\sqrt{3}$.将△ABC沿直线CB向右作无滑动滚动一次,则点C经过的路径长是$\frac{5π}{2}$.
如图,△ABC中,∠C=90°,∠A=60°,AB=2$\sqrt{3}$.将△ABC沿直线CB向右作无滑动滚动一次,则点C经过的路径长是$\frac{5π}{2}$.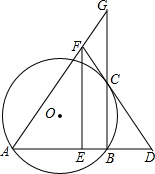 如图,已知:AB是⊙O的弦,过点B作BC⊥AB交⊙O于点C,过点C作⊙O的切线交AB的延长线于点D,取AD的中点E,过点E作EF∥BC交DC的延长线于点F,连接AF并延长交BC的延长线于点G.
如图,已知:AB是⊙O的弦,过点B作BC⊥AB交⊙O于点C,过点C作⊙O的切线交AB的延长线于点D,取AD的中点E,过点E作EF∥BC交DC的延长线于点F,连接AF并延长交BC的延长线于点G.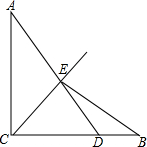 如图,AC⊥BC,AC=BC,D是BC上一点,连接AD,与∠ACB的平分线交于点E,连接BE.若S△ACE=$\frac{6}{7}$,S△BDE=$\frac{3}{14}$,则AC=2.
如图,AC⊥BC,AC=BC,D是BC上一点,连接AD,与∠ACB的平分线交于点E,连接BE.若S△ACE=$\frac{6}{7}$,S△BDE=$\frac{3}{14}$,则AC=2.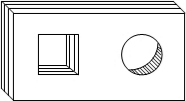 如图,是一个带有方形空洞和圆形空洞的儿童玩具,如果用下列几何体作为塞子,那么既可以堵住方形空洞,又可以堵住圆形空洞的几何体是( )
如图,是一个带有方形空洞和圆形空洞的儿童玩具,如果用下列几何体作为塞子,那么既可以堵住方形空洞,又可以堵住圆形空洞的几何体是( )