题目内容
18.已知关于x的方程(x-3)(x-2)-p2=0.(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1,x2,且满足x12+x22=3x1x2,求实数p的值.
分析 (1)化成一般形式,求根的判别式,当△>0时,方程总有两个不相等的实数根;
(2)根据根与系的关系求出两根和与两根积,再把${{x}_{1}}^{2}+{{x}_{2}}^{2}=3{x}_{1}{x}_{2}$变形,化成和与乘积的形式,代入计算,得到一个关于p的一元二次方程,解方程.
解答 证明:(1)(x-3)(x-2)-p2=0,
x2-5x+6-p2=0,
△=(-5)2-4×1×(6-p2)=25-24+4p2=1+4p2,
∵无论p取何值时,总有4p2≥0,
∴1+4p2>0,
∴无论p取何值时,方程总有两个不相等的实数根;
(2)x1+x2=5,x1x2=6-p2,
∵x12+x22=3x1x2,
∴(x1+x2)2-2x1x2=3x1x2,
∴52=5(6-p2),
∴p=±1.
点评 本题考查了根的判别式和根与系数的关系,注意熟记以下知识点:
(1)一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;
②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.
上面的结论反过来也成立.
(2)一元二次方程ax2+bx+c=0(a≠0)的两实数根分别为x1,x2,则有${x}_{1}+{x}_{2}=-\frac{b}{a}$,${x}_{1}{x}_{2}=\frac{c}{a}$.

练习册系列答案
相关题目
3.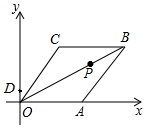 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )| A. | (0,0) | B. | (1,$\frac{1}{2}$) | C. | ($\frac{6}{5}$,$\frac{3}{5}$) | D. | ($\frac{10}{7}$,$\frac{5}{7}$) |
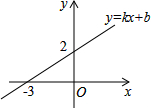 一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是x>-3.
一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是x>-3.
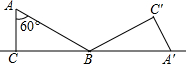 如图,△ABC中,∠C=90°,∠A=60°,AB=2$\sqrt{3}$.将△ABC沿直线CB向右作无滑动滚动一次,则点C经过的路径长是$\frac{5π}{2}$.
如图,△ABC中,∠C=90°,∠A=60°,AB=2$\sqrt{3}$.将△ABC沿直线CB向右作无滑动滚动一次,则点C经过的路径长是$\frac{5π}{2}$.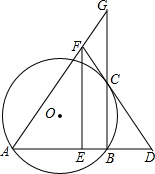 如图,已知:AB是⊙O的弦,过点B作BC⊥AB交⊙O于点C,过点C作⊙O的切线交AB的延长线于点D,取AD的中点E,过点E作EF∥BC交DC的延长线于点F,连接AF并延长交BC的延长线于点G.
如图,已知:AB是⊙O的弦,过点B作BC⊥AB交⊙O于点C,过点C作⊙O的切线交AB的延长线于点D,取AD的中点E,过点E作EF∥BC交DC的延长线于点F,连接AF并延长交BC的延长线于点G.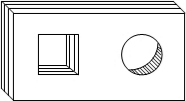 如图,是一个带有方形空洞和圆形空洞的儿童玩具,如果用下列几何体作为塞子,那么既可以堵住方形空洞,又可以堵住圆形空洞的几何体是( )
如图,是一个带有方形空洞和圆形空洞的儿童玩具,如果用下列几何体作为塞子,那么既可以堵住方形空洞,又可以堵住圆形空洞的几何体是( )