题目内容
1. 如图,在矩形ABCD中,对角线AC、BD交于点O,以下结论错误的是( )
如图,在矩形ABCD中,对角线AC、BD交于点O,以下结论错误的是( )| A. | ∠ABC=90° | B. | △OAD是等边三角形 | ||
| C. | OA=OB;OC=OB | D. | AC=BD |
分析 根据矩形的对角线互相平分且相等,四个角都是直角对各选项分析判断利用排除法求解.
解答 解:∵四边形ABCD是矩形,
∴AC=BD,OA=OC=OB=OD,∠DAB=∠ABC=∠BCD=∠CDA=90°,
∴A、C、D各项结论都正确,
而△OAD是等边三角形不一定成立,
故选:B.
点评 本题考查了矩形的性质;熟练掌握矩形的性质是解决问题的关键.

练习册系列答案
相关题目
11.已知在△ABC中,AB=AC,AD是角平分线,点D在边BC上,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AC}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )
| A. | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ | C. | -$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ |
 如图,平行四边形ABCD对角线交于点O,若AC=6cm,BC=10cm,BD=24cm,则△OBC的周长为25cm.
如图,平行四边形ABCD对角线交于点O,若AC=6cm,BC=10cm,BD=24cm,则△OBC的周长为25cm.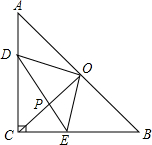 如图,在等腰直角△ABC中,∠ACB=90°,CO⊥AB于点O,点D、E分别在边AC、BC上,且AD=CE,连结DE交CO于点P,给出以下结论:
如图,在等腰直角△ABC中,∠ACB=90°,CO⊥AB于点O,点D、E分别在边AC、BC上,且AD=CE,连结DE交CO于点P,给出以下结论: 如图,正方形ABCD中,以对角线AC为一边作菱形AEFC,则∠FAB=22.5°.
如图,正方形ABCD中,以对角线AC为一边作菱形AEFC,则∠FAB=22.5°.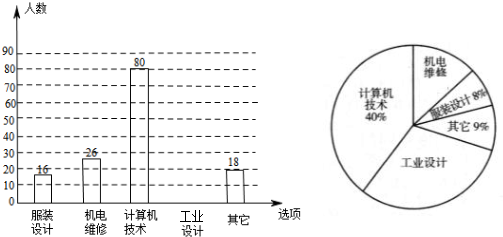
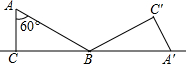 如图,△ABC中,∠C=90°,∠A=60°,AB=2$\sqrt{3}$.将△ABC沿直线CB向右作无滑动滚动一次,则点C经过的路径长是$\frac{5π}{2}$.
如图,△ABC中,∠C=90°,∠A=60°,AB=2$\sqrt{3}$.将△ABC沿直线CB向右作无滑动滚动一次,则点C经过的路径长是$\frac{5π}{2}$.