题目内容
5．
如图，在?ABCD中，AF与对角线BD垂直于F，AE⊥CD，E是垂足．AB=6，AE=8，BD=12．求AF的长．
分析 由在?ABCD中，AE⊥CD，AB=6，AE=8，即可求得?ABCD的面积，继而求得△ABD的面积，又由三角形的面积公式可得：S△ABD=$\frac{1}{2}$BD•AF=24，继而求得答案．
解答 解：∵四边形ABCD是平行四边形，
∴AB=CD=6，
∵AE⊥CD，AE=8，
∴S?ABCD=AB•CD=48，
∴S△ABD=$\frac{1}{2}$S?ABCD=24，
∵AF⊥BD，BD=12，
∴S△ABD=$\frac{1}{2}$BD•AF=24，
∴AF=4．
点评 此题考查了平行四边形的性质．注意利用面积求解是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
16．在一个不透明的布袋中装有2个白球和1个红球，它们除了颜色不同外，其余均相同．从中随机摸出一个球，摸到红球的概率是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{1}{3}$ | C． | $\frac{3}{8}$ | D． | $\frac{5}{8}$ |
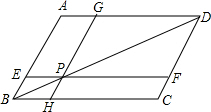如图，已知?ABCD，点P在对角线BD上，EF∥BC，GH∥AB，点E，H，F，G分别在边AB，BC，CD，AD上，图中哪两个平行四边形的面积相等？试证明你的结论．
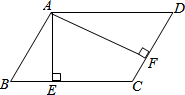已知?ABCD的周长为36cm，过点A作AE⊥BC，AF⊥CD，若AE=2cm，AF=4cm，求平行四边形各边的长．