题目内容
8.计算:(1)3$\sqrt{3}$-$\sqrt{8}$+$\sqrt{2}$-$\sqrt{27}$
(2)(4$\sqrt{6}$-6$\sqrt{2}$)×2$\sqrt{2}$
(3)$\sqrt{14}$÷$\sqrt{6}$×$\sqrt{\frac{27}{2}}$
(4)($\sqrt{0.5}$+2$\sqrt{\frac{1}{3}}$)-($\sqrt{\frac{1}{8}}$-$\sqrt{75}$)
(5)(3$\sqrt{3}$+2$\sqrt{5}$)(3$\sqrt{3}$-2$\sqrt{5}$)
(6)(5$\sqrt{48}$-6$\sqrt{27}$+4$\sqrt{15}$)÷$\sqrt{3}$.
分析 (1)先把二次根式化为最简二次根式,然后合并即可;
(2)利用二次根式的乘法法则运算;
(3)利用二次根式的乘除法则运算;
(4)先把二次根式化为最简二次根式,然后合并即可;
(5)利用平方差公式计算;
(6)利用二次根式的除法法则运算.
解答 解:(1)原式=3$\sqrt{3}$-2$\sqrt{2}$+$\sqrt{2}$-3$\sqrt{3}$
=-$\sqrt{2}$;
(2)原式=8$\sqrt{6×2}$-12$\sqrt{2×2}$
=16$\sqrt{3}$-24;
(3)原式=$\sqrt{14×\frac{1}{6}×\frac{27}{2}}$
=$\frac{3\sqrt{14}}{2}$;
(4)原式=$\frac{\sqrt{2}}{2}$+$\frac{2\sqrt{3}}{3}$-$\frac{\sqrt{2}}{4}$+5$\sqrt{3}$
=$\frac{\sqrt{2}}{4}$+$\frac{17\sqrt{3}}{3}$;
(5)原式=27-20
=7;
(6)原式=5$\sqrt{48÷3}$-6$\sqrt{27÷3}$+4$\sqrt{15÷3}$
=20-18+4$\sqrt{5}$
=2+4$\sqrt{5}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
3.二次根式$\sqrt{a{x}^{2}+bx+c}$(a2+b2≠0)对于x的任何值都无意义的条件是( )
| A. | a>0,△>0 | B. | a>0,△<0 | C. | a<0,△>0 | D. | a<0,△<0 |
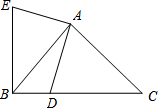 在等腰 Rt△ABC中,∠A=90°,AC=AB=2,D是BC边上的点且BD=$\frac{1}{3}$CD,连接AD.AD⊥AE,AE=AD,连接BE.下列结论:
在等腰 Rt△ABC中,∠A=90°,AC=AB=2,D是BC边上的点且BD=$\frac{1}{3}$CD,连接AD.AD⊥AE,AE=AD,连接BE.下列结论: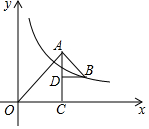 如图,点C在x轴的正半釉上,且∠ACO=90°,CO=CA,点D在边AC上,在边AC的右侧取一点B,使∠ADB=90°,且BD=DA,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若S△OAC-S△BAD=5k-2,则k的值为$\frac{4}{9}$.
如图,点C在x轴的正半釉上,且∠ACO=90°,CO=CA,点D在边AC上,在边AC的右侧取一点B,使∠ADB=90°,且BD=DA,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若S△OAC-S△BAD=5k-2,则k的值为$\frac{4}{9}$.