题目内容
13.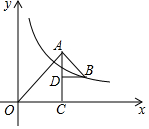 如图,点C在x轴的正半釉上,且∠ACO=90°,CO=CA,点D在边AC上,在边AC的右侧取一点B,使∠ADB=90°,且BD=DA,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若S△OAC-S△BAD=5k-2,则k的值为$\frac{4}{9}$.
如图,点C在x轴的正半釉上,且∠ACO=90°,CO=CA,点D在边AC上,在边AC的右侧取一点B,使∠ADB=90°,且BD=DA,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若S△OAC-S△BAD=5k-2,则k的值为$\frac{4}{9}$.
分析 设△OAC和△BAD的直角边长分别为a、b,结合等腰直角三角形的性质及图象可得出点B的坐标,根据三角形的面积公式结合反比例函数系数k的几何意义得出方程$\frac{1}{2}$k=5k-2,解方程即可.
解答 解:设△OAC和△BAD的直角边长分别为a、b,则点B的坐标为(a+b,a-b).
∵反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,
∴S△OAC-S△BAD=$\frac{1}{2}$a2-$\frac{1}{2}$b2=$\frac{1}{2}$(a+b)×(a-b)=$\frac{1}{2}$k.
∵S△OAC-S△BAD=5k-2,
∴$\frac{1}{2}$k=5k-2,解得k=$\frac{4}{9}$.
故答案为$\frac{4}{9}$.
点评 本题考查了反比例函数系数k的几何意义、等腰三角形的性质以及三角形面积公式的运用,解题的关键是设等腰直角三角形的直角边分别为a、b,用其表示出反比例函数上点的坐标.

练习册系列答案
相关题目
3.计算2x3÷$\frac{1}{x}$的结果是( )
| A. | 2x2 | B. | 2x4 | C. | 2x | D. | 4 |
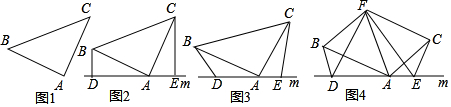
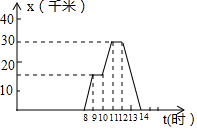 请根据图编写一道题,并给出解答.
请根据图编写一道题,并给出解答.