题目内容
16. 已知,如图,OP是∠MON的平分线,PA⊥OM,PB⊥ON,A、B分别为垂足,点C、D分别在OA、OB上,∠CPD=$\frac{1}{2}$∠APB.
已知,如图,OP是∠MON的平分线,PA⊥OM,PB⊥ON,A、B分别为垂足,点C、D分别在OA、OB上,∠CPD=$\frac{1}{2}$∠APB.求证:PD是∠BDC的平分线.
分析 在ON上截取BE=AC,连接PE,根据角平分线的性质得出PA=PB,进而通过证得△PAC≌△PBE,证得
PC=PE,∠APC=∠BPE,进一步证得∠CPD=∠EPD,然后证得△CPD≌△EPD,即可证得结论.
解答  证明:在ON上截取BE=AC,连接PE,
证明:在ON上截取BE=AC,连接PE,
∵PA⊥OM,PB⊥ON,OP是∠MON的平分线,
∴PA=PB,
在△PAC和△PBE中,
$\left\{\begin{array}{l}{PA=PB}\\{∠PAC=∠PBE=90°}\\{AC=BE}\end{array}\right.$
∴△PAC≌△PBE(SAS),
∴PC=PE,∠APC=∠BPE,
∵∠CPD=$\frac{1}{2}$∠APB,
∴∠APC+∠BPD=$\frac{1}{2}$∠APB,
∴∠BPE+∠BPD=$\frac{1}{2}$∠APB,
∴∠CPD=∠EPD,
在△CPD和△EPD中
$\left\{\begin{array}{l}{PC=PE}\\{∠CPD=∠EPD}\\{PD=PD}\end{array}\right.$
∴△CPD≌△EPD(SAS),
∴∠CDP=∠EDP,
∴PD是∠BDC的平分线.
点评 本题考查了角平分线的性质,三角形全等的判定和性质,作出辅助线构建全等三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.小丽连续两次掷一个质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数.则两次向上的一面的点数之和大于3的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{11}{12}$ | C. | $\frac{31}{36}$ | D. | $\frac{2}{3}$ |
 如图为一个正方体的展开图,图中已标出三个面在正方体中的位置f表示前面,r表示右面,d表示下面.试判定另外三个面a、b、c在正方体中的位置.
如图为一个正方体的展开图,图中已标出三个面在正方体中的位置f表示前面,r表示右面,d表示下面.试判定另外三个面a、b、c在正方体中的位置. 如图,AB是⊙O的直径,DA、CB是⊙O的切线,CD切⊙O于E.
如图,AB是⊙O的直径,DA、CB是⊙O的切线,CD切⊙O于E. 如图,两个圆是以点O为圆心的同心圆,大圆的弦AB是小圆的切线,C为切点,C是AB的中点吗?为什么?
如图,两个圆是以点O为圆心的同心圆,大圆的弦AB是小圆的切线,C为切点,C是AB的中点吗?为什么?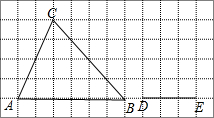 如图,在12×6的正方形网格中,点A,B,C,D,E均在格点上,以DE为一边画格点△DEF,使得△DEF∽△ABC.其中AB=6,AC=2$\sqrt{5}$,BC=4$\sqrt{2}$,DE=3.
如图,在12×6的正方形网格中,点A,B,C,D,E均在格点上,以DE为一边画格点△DEF,使得△DEF∽△ABC.其中AB=6,AC=2$\sqrt{5}$,BC=4$\sqrt{2}$,DE=3. (1)若a,b两数在数轴上的表示如下:
(1)若a,b两数在数轴上的表示如下: