题目内容
1.先阅读下列解题过程,然后解答问题(1)、(2)解方程:|x+3|=2.
解:当x+3≥0时,原方程可化为:x+3=2,解得x=-1;
当x+3<0时,原方程可化为:x+3=-2,解得x=-5.
所以原方程的解是x=-1,x=-5.
(1)解方程:|3x-2|+x=0;
(2)探究:当b为何值时,方程|x-2|=b+1 ①无解;②只有一个解;③有两个解.
分析 (1)分两种情况:x≥0,x<0探讨得出答案即可;
(2)由题意可知:①无解b+1<0;②只有一个解b+1=0;③有两个解b+1>0,分别求得答案即可.
解答 解:(1)|3x-2|+x=0;
当x≥0时,此方程不成立;
当x<0时,原方程化为-3x+2+x=0,解得:x=1,不合题意,
所以此方程无解;
(2)|x-2|=b+1
①无解b+1<0,b<-1;②只有一个解b+1=0,b=-1;③有两个解b+1>0,b>-1.
点评 此题考查含绝对值的一元一次方程,掌握绝对值的意义是解决问题的关键.

练习册系列答案
相关题目
13.下列计算中错误的是( )
| A. | x2•x3=x6 | B. | (-x)2=x2 | C. | x4÷x4=1 | D. | (x2)2=x4 |
10.代数式-$\frac{3}{5}{x}^{2}{y}^{3}$的系数是( )
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | -3 | D. | -5 |

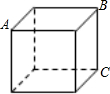 如图,一只蚂蚁要从正方体得一个顶点A沿表面爬行到顶点B,则沿线段AB爬行,就可以爬行路线最短,这其中的道理是两点之间,线段最短.
如图,一只蚂蚁要从正方体得一个顶点A沿表面爬行到顶点B,则沿线段AB爬行,就可以爬行路线最短,这其中的道理是两点之间,线段最短.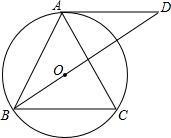 如图,△ABC中,AB=AC,⊙O为△ABC的外接圆,延长BO交⊙O的切线于D,求证:AD∥BC.
如图,△ABC中,AB=AC,⊙O为△ABC的外接圆,延长BO交⊙O的切线于D,求证:AD∥BC. 已知,如图,OP是∠MON的平分线,PA⊥OM,PB⊥ON,A、B分别为垂足,点C、D分别在OA、OB上,∠CPD=$\frac{1}{2}$∠APB.
已知,如图,OP是∠MON的平分线,PA⊥OM,PB⊥ON,A、B分别为垂足,点C、D分别在OA、OB上,∠CPD=$\frac{1}{2}$∠APB.