题目内容
11. 如图,两个圆是以点O为圆心的同心圆,大圆的弦AB是小圆的切线,C为切点,C是AB的中点吗?为什么?
如图,两个圆是以点O为圆心的同心圆,大圆的弦AB是小圆的切线,C为切点,C是AB的中点吗?为什么?
分析 根据切线的性质得出OC⊥AB,根据垂径定理可知AC=BC.
解答 解:点C是AB的中点.
理由:如图,连接OC,
∵大圆的弦AB是小圆的切线,点C为切点,
∴OC⊥AB.
∵OC⊥AB,
∴AC=BC.
∴点C是AB的中点.
点评 本题主要考查的是切线的性质、垂径定理的应用,掌握本题的辅助线的作法是解题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
19.下列说法中正确的是( )
| A. | 若mx=my,则x=y | B. | 若x=y,则$\frac{x}{{m}^{2}}$=$\frac{y}{{m}^{2}}$ | ||
| C. | 若$\frac{x}{m}$=$\frac{y}{m}$,则x=y | D. | 若x2=y2,则x3=y3 |
20.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  等边三角形 | B. |  等腰梯形 | C. |  平行四边形 | D. |  正方形 |
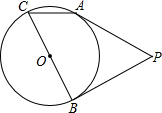 如图,PA,PB切⊙O于点A,B,BC是⊙O的直径,∠C=55°,则∠P=50°.
如图,PA,PB切⊙O于点A,B,BC是⊙O的直径,∠C=55°,则∠P=50°. 已知,如图,OP是∠MON的平分线,PA⊥OM,PB⊥ON,A、B分别为垂足,点C、D分别在OA、OB上,∠CPD=$\frac{1}{2}$∠APB.
已知,如图,OP是∠MON的平分线,PA⊥OM,PB⊥ON,A、B分别为垂足,点C、D分别在OA、OB上,∠CPD=$\frac{1}{2}$∠APB.