题目内容
4. 如图,AB是⊙O的直径,DA、CB是⊙O的切线,CD切⊙O于E.
如图,AB是⊙O的直径,DA、CB是⊙O的切线,CD切⊙O于E.(1)若AD=4,BC=9,求⊙O的半径R;
(2)若OD=6.OC=8,求⊙O的半径R.
分析 (1)由切线长定理可知AD=DE,从而可证明△ADO≌△EDO,于是得到∠DOE=$\frac{1}{2}$∠AOE,同理:∠EOC=$\frac{1}{2}$∠EOB,∠DOE+∠EOC=$\frac{1}{2}$(∠AOE+∠EOB)=90°,然后证明△OAD∽△BOC,从而可求得R=6;
(2)由勾股定理先求得DC=10,然后利用面积法可求得OE=4.8,即R=4.8.
解答 解:如图1所示;连接OE.
∵DA、DE是圆O的切线,
∴AD=ED.
在△ADO和△EDO中,
$\left\{\begin{array}{l}{AD=DE}\\{OA=OE}\\{OD=OD}\end{array}\right.$,
∴△ADO≌△EDO.
∴∠AOD=∠EOD.
∴∠DOE=$\frac{1}{2}$∠AOE.
同理:∠EOC=$\frac{1}{2}$∠EOB.
∴∠DOE+∠EOC=$\frac{1}{2}$(∠AOE+∠EOB)=90°.
∴∠AOD+∠BOC=90°.
∵AD、BC是圆O的切线,AB是圆O的直径,
∴∠DAO=∠OBC=90°.
∴∠ADO+∠AOD=90°.
∴∠ADO=∠BOC.
∴△OAD∽△BOC.
∴$\frac{AD}{OA}=\frac{OB}{BC}$.
∴$\frac{4}{R}=\frac{R}{9}$.
解得:R=6.
(2)如图1所示:由(1)可知△DOC为直角三角形.
在Rt△DOC中,由勾股定理得:DC=$\sqrt{O{D}^{2}+O{C}^{2}}$=10.
∵$\frac{1}{2}DC•OE=\frac{1}{2}DO•OC$,
∴$\frac{1}{2}×10×OE=\frac{1}{2}×6×8$.
解得:OE=4.8.
∴R=4.8.
点评 本题考查了切线的性质,全等三角形的判定和性质,证得∠DOC=90°,从而得到△OAD∽△BOC是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 若mx=my,则x=y | B. | 若x=y,则$\frac{x}{{m}^{2}}$=$\frac{y}{{m}^{2}}$ | ||
| C. | 若$\frac{x}{m}$=$\frac{y}{m}$,则x=y | D. | 若x2=y2,则x3=y3 |
| A. | x2•x3=x6 | B. | (-x)2=x2 | C. | x4÷x4=1 | D. | (x2)2=x4 |
| A. | -8 | B. | -3$\frac{1}{2}$ | C. | 0.66666… | D. | π |
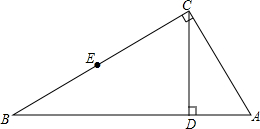 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,CD⊥AB于D点,其中E是BC的中点,以C为圆心,CD为半径作⊙C,则A,B,C,D,E五个点中,点A、B在⊙C外,点E、D在⊙C上,点C在⊙C内.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,CD⊥AB于D点,其中E是BC的中点,以C为圆心,CD为半径作⊙C,则A,B,C,D,E五个点中,点A、B在⊙C外,点E、D在⊙C上,点C在⊙C内.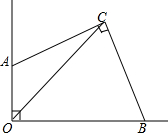 如图,若∠AOB=∠ACB=90°,OC平分∠AOB.
如图,若∠AOB=∠ACB=90°,OC平分∠AOB.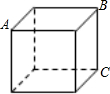 如图,一只蚂蚁要从正方体得一个顶点A沿表面爬行到顶点B,则沿线段AB爬行,就可以爬行路线最短,这其中的道理是两点之间,线段最短.
如图,一只蚂蚁要从正方体得一个顶点A沿表面爬行到顶点B,则沿线段AB爬行,就可以爬行路线最短,这其中的道理是两点之间,线段最短.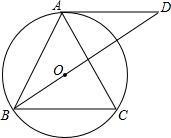 如图,△ABC中,AB=AC,⊙O为△ABC的外接圆,延长BO交⊙O的切线于D,求证:AD∥BC.
如图,△ABC中,AB=AC,⊙O为△ABC的外接圆,延长BO交⊙O的切线于D,求证:AD∥BC. 已知,如图,OP是∠MON的平分线,PA⊥OM,PB⊥ON,A、B分别为垂足,点C、D分别在OA、OB上,∠CPD=$\frac{1}{2}$∠APB.
已知,如图,OP是∠MON的平分线,PA⊥OM,PB⊥ON,A、B分别为垂足,点C、D分别在OA、OB上,∠CPD=$\frac{1}{2}$∠APB.