题目内容
7.一次函数y=x+1与y=ax+3的图象交于点P,且点P的横坐标为1,则关于x,y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=ax+3}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.分析 先把x=1代入y=x+1,得出y=2,则两个一次函数的交点P的坐标为(1,2);那么交点坐标同时满足两个函数的解析式,而所求的方程组正好是由两个函数的解析式所构成,因此两函数的交点坐标即为方程组的解.
解答  解:把x=1代入y=x+1,得出y=2,
解:把x=1代入y=x+1,得出y=2,
函数y=x+1和y=ax+3的图象交于点P(1,2),
即x=1,y=2同时满足两个一次函数的解析式.
所以关于x,y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=ax+3}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
故答案为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
点评 本题考查了一次函数与二元一次方程组的联系,方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的一次函数式,因此方程组的解就是两个相应的一次函数图象的交点坐标.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
18. 下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
 下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
下面四个图形中,经过折叠能围成如图所示的几何图形的是( )| A. |  | B. |  | C. |  | D. |  |
15.下列运算正确的是( )
| A. | (-a)3÷(-a)=a2 | B. | (a2)3=a5 | C. | a2•a3=a6 | D. | a3+a2=a5 |
 已知:如图,在△ABC中,AB=AC,点D、E、F分别在边BC、AC、AB上,且有BF=CD,BD=CE.
已知:如图,在△ABC中,AB=AC,点D、E、F分别在边BC、AC、AB上,且有BF=CD,BD=CE.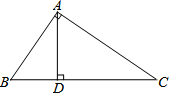 如图,在Rt△ABC中,AB=3,BC=6,AD⊥BC,垂足为D,则BD的长为$\frac{3}{2}$.
如图,在Rt△ABC中,AB=3,BC=6,AD⊥BC,垂足为D,则BD的长为$\frac{3}{2}$.