题目内容
17．
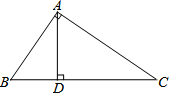如图，在Rt△ABC中，AB=3，BC=6，AD⊥BC，垂足为D，则BD的长为$\frac{3}{2}$．
分析 根据直角三角形的性质得到∠C=30°，根据同角的余角相等得到∠BAD=∠C=30°，根据直角三角形的性质解答即可．
解答 解：∵∠BAC=90°，AB=3，BC=6，
∴∠C=30°，
∵∠BAC=90°，AD⊥BC，
∴∠BAD=∠C=30°，
∴BD=$\frac{1}{2}$AB=$\frac{3}{2}$，
故答案为：$\frac{3}{2}$．
点评 本题考查的是直角三角形得到性质，掌握30°所对的直角边是斜边的一半是解题的关键．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
请你在数轴上画出表示$\sqrt{2}$的点（保留作图痕迹）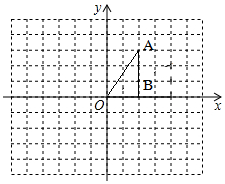
如图，点A的坐标为（2，3），点B的坐标为（2，0），作如下操作；
如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F，则下列结论：