题目内容
17.抛物线y=$\frac{1}{2}$x2-kx+k与直线y=2x-1的两个交点距离最近时,k的取值为-1.分析 设抛物线与直线的两个交点为(x1,y1)、(x2,y2),则y1=2x1-1,y2=2x2-1,由由$\left\{\begin{array}{l}{y=\frac{1}{2}{x}^{2}-kx+k}\\{y=2x-1}\end{array}\right.$得$\frac{1}{2}$x2-kx+k=2x-1,可得x1+x2=2(k+2),x1x2=2(k+1),将其代入到d=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$=$\sqrt{5[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$,可得d=$\sqrt{20(k+1)^{2}+20}$,据此可得k=-1时,d取得最小值.
解答 解:设抛物线与直线的两个交点为(x1,y1)、(x2,y2),
其中y1=2x1-1,y2=2x2-1,
由$\left\{\begin{array}{l}{y=\frac{1}{2}{x}^{2}-kx+k}\\{y=2x-1}\end{array}\right.$得$\frac{1}{2}$x2-kx+k=2x-1,
即x2-2(k+2)x+2(k+1)=0,
∴x1+x2=2(k+2),x1x2=2(k+1),△=[-2(k+2)]2-4×1×2(k+1)≥0,即k2+2k+2≥0
∴k为全体实数,
则两交点间的距离d=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$
=$\sqrt{({x}_{1}-{x}_{2})^{2}+(2{x}_{1}-1-2{x}_{2}+1)^{2}}$
=$\sqrt{({x}_{1}-{x}_{2})^{2}+4({x}_{1}-{x}_{2})^{2}}$
=$\sqrt{5[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$
=$\sqrt{5[4(k+2)^{2}-8(k+1)]}$
=$\sqrt{20(k+1)^{2}+20}$,
∴当k=-1时,d取得最小值,最小值为1,
故答案为:-1.
点评 本题主要考查抛物线与直线的交点问题、两点间的距离公式及二次函数的性质,根据题意得出两点间的距离关于k的表达式是解题的关键.

 快捷英语周周练系列答案
快捷英语周周练系列答案| A. | 教室第三排 | B. | 湖心南路 | ||
| C. | 南偏东40° | D. | 东经112°,北纬51° |
| A. | 由a=b,得到1-a=1-b | B. | 由$\frac{a}{2}$=$\frac{b}{2}$,得到a=b | ||
| C. | 由a=b,得到ac=bc | D. | 由ac=bc,得到a=b |

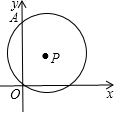 如图,点P(1,2),⊙P经过原点O,交y轴正半轴于点A,点B在⊙P上,∠BAO=45°,则点B的坐标是(3,1)或(-1,3).
如图,点P(1,2),⊙P经过原点O,交y轴正半轴于点A,点B在⊙P上,∠BAO=45°,则点B的坐标是(3,1)或(-1,3). 如图,二次函数y1=ax2+bx+c与反比例函数y2=$\frac{k}{x}$的图象交于A(-1.5,p),B(1,q),C(2.5,r)三点,则当y1<y2时,x的取值范围是-1.5<x<0或1<x<2.5.
如图,二次函数y1=ax2+bx+c与反比例函数y2=$\frac{k}{x}$的图象交于A(-1.5,p),B(1,q),C(2.5,r)三点,则当y1<y2时,x的取值范围是-1.5<x<0或1<x<2.5.