题目内容
8.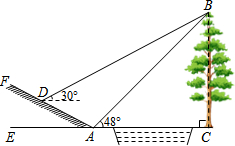 如图所示,小河中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.若斜坡FA的坡比i=1:$\sqrt{3}$,求大树的高度.(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,$\sqrt{3}$≈1.73)
如图所示,小河中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.若斜坡FA的坡比i=1:$\sqrt{3}$,求大树的高度.(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,$\sqrt{3}$≈1.73)
分析 首先过点D作DM⊥BC于点M,DN⊥AC于点N,由FA的坡比i=1:$\sqrt{3}$,DA=6,可求得AN与DN的长,然后设大树的高度为x,又由在斜坡上A处测得大树顶端B的仰角是48°,可得AC=$\frac{x}{1.11}$,又由在△ADM中,$\frac{AM}{DM}$=$\frac{\sqrt{3}}{3}$,可得x-3=(3$\sqrt{3}$+$\frac{x}{1.11}$)•$\frac{\sqrt{3}}{3}$,继而求得答案.
解答 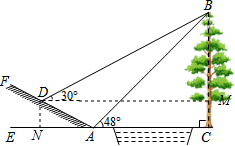 解:过点D作DM⊥BC于点M,DN⊥AC于点N,
解:过点D作DM⊥BC于点M,DN⊥AC于点N,
则四边形DMCN是矩形,
∵DA=6,斜坡FA的坡比i=1:$\sqrt{3}$,
∴DN=$\frac{1}{2}$AD=3,AN=AD•cos30°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
设大树的高度为x,
∵在斜坡上A处测得大树顶端B的仰角是48°,
∴tan48°=$\frac{BC}{AC}$≈1.11,
∴AC=$\frac{x}{1.1}$,
∴DM=CN=AN+AC=3$\sqrt{3}$+$\frac{x}{1.11}$,
∵在△ADM中,$\frac{AM}{DM}$=$\frac{\sqrt{3}}{3}$,
∴x-3=(3$\sqrt{3}$+$\frac{x}{1.11}$)•$\frac{\sqrt{3}}{3}$,
解得:x≈13.
答:树高BC约13米.
点评 本题考查了仰角、坡角的定义,解直角三角形的应用,能借助仰角构造直角三角形,并结合图形利用三角函数解直角三角形是解题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 如图,已知点O(0,0),A(-4,-1),线段AB与x轴平行,且AB=2,抛物线l:y=-x2+mx+n(m,n为常数)经过点C(0,3)和D(3,0)
如图,已知点O(0,0),A(-4,-1),线段AB与x轴平行,且AB=2,抛物线l:y=-x2+mx+n(m,n为常数)经过点C(0,3)和D(3,0)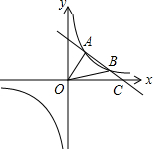 如图,已知A(a,a+1),B(a+3,a-1)是反比例函数y=$\frac{k}{x}$的图象上两点,必过A、B的直线y=mx+n交x轴于点C.
如图,已知A(a,a+1),B(a+3,a-1)是反比例函数y=$\frac{k}{x}$的图象上两点,必过A、B的直线y=mx+n交x轴于点C.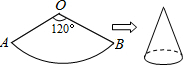 如图,一个扇形铁皮OAB,已知OA=12cm,∠AOB=120°,小华将OA、OB合拢制成了一个圆锥形烟囱帽(接缝处忽略不计),则烟囱帽的高为8$\sqrt{2}$cm.
如图,一个扇形铁皮OAB,已知OA=12cm,∠AOB=120°,小华将OA、OB合拢制成了一个圆锥形烟囱帽(接缝处忽略不计),则烟囱帽的高为8$\sqrt{2}$cm.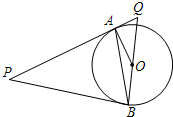 如图所示.P是⊙O外一点.PA是⊙O的切线.A是切点.B是⊙O上一点.且PA=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.
如图所示.P是⊙O外一点.PA是⊙O的切线.A是切点.B是⊙O上一点.且PA=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q. A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.
A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.