题目内容
20.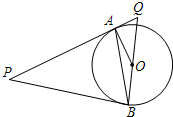 如图所示.P是⊙O外一点.PA是⊙O的切线.A是切点.B是⊙O上一点.且PA=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.
如图所示.P是⊙O外一点.PA是⊙O的切线.A是切点.B是⊙O上一点.且PA=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.(1)求证:PB是⊙O的切线;
(2)求证:AQ•PQ=OQ•BQ;
(3)设∠AOQ=α,若cosα=$\frac{4}{5}$,OQ=10,求BP的长.
分析 (1)连接OP,与AB交于点C.欲证明PB是⊙O的切线,只需证明∠OBP=90°即可;
(2)根据相似三角形的判定定理AA证明△QAO∽△QBP,然后由相似三角形的对应边成比例求得$\frac{AQ}{BQ}=\frac{OQ}{PQ}$,即可得到结论;
(3)在Rt△OAQ中根据勾股定理和三角函数的余弦值的定义解得QB=18,利用(1)的结论求得PQ=30,根据线段的和差即可得到结论.
解答 (1)证明:连接OP,与AB交于点C.
∵PA=PB,OA=OB,OP=OP,
∴△OAP≌△OBP(SSS),
∴∠OBP=∠OAP,
∵PA是⊙O的切线,A是切点,
∴∠OAP=90°,
∴∠OBP=90°,即PB是⊙O的切线;
(2)证明:∵∠Q=∠Q,∠OAQ=∠QBP=90°,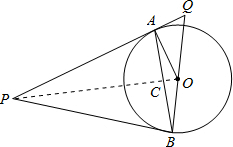
∴△QAO∽△QBP,
∴$\frac{AQ}{BQ}=\frac{OQ}{PQ}$,
即AQ•PQ=OQ•BQ;
(3)连结OP交AB于点C,
在Rt△OAQ中,∵OQ=10,cosα=$\frac{4}{5}$,
∴OA=8,AQ=6,
∴QB=18;
∵$\frac{AQ}{BQ}=\frac{OQ}{PQ}$,
∴PQ=30,即PA=24,
∴PB=PA=24.
点评 本题综合考查了切线的判定与性质、相似三角形与全等三角形的判定与性质、解直角三角形以及勾股定理.图形中的线段的求法,可以通过特殊角的三角函数值、切线的有关知识及勾股定理求解.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
15.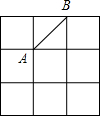 在边长为2的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为2的概率为( )
在边长为2的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为2的概率为( )
 在边长为2的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为2的概率为( )
在边长为2的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为2的概率为( )| A. | $\frac{3}{16}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{5}{16}$ |
5.若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )
| A. | 矩形 | B. | 菱形 | ||
| C. | 对角线相等的四边形 | D. | 对角线互相垂直的四边形 |
9.若反比例函数y=$\frac{k}{x}$的图象经过点(-3,2),则反比例函数y=-$\frac{k}{x}$的图象在( )
| A. | 一、二象限 | B. | 三、四象限 | C. | 一、三象限 | D. | 二、四象限 |
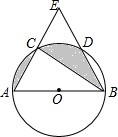 如图,AB是⊙O的直径,点C,D是圆的三等分点,AC,BD的延长线交于点E,若CE=2,则⊙O中阴影部分的面积为$\frac{4}{3}$π-$\sqrt{3}$.
如图,AB是⊙O的直径,点C,D是圆的三等分点,AC,BD的延长线交于点E,若CE=2,则⊙O中阴影部分的面积为$\frac{4}{3}$π-$\sqrt{3}$.
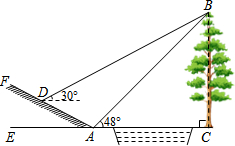 如图所示,小河中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.若斜坡FA的坡比i=1:$\sqrt{3}$,求大树的高度.(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,$\sqrt{3}$≈1.73)
如图所示,小河中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.若斜坡FA的坡比i=1:$\sqrt{3}$,求大树的高度.(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,$\sqrt{3}$≈1.73)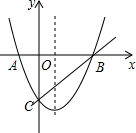 如图,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(-1,0),点C的坐标是(0,-3).
如图,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(-1,0),点C的坐标是(0,-3). 数字a、b在数轴上的位置如图所示,试化简$\sqrt{(b-a)^{2}}$+|2-a|.
数字a、b在数轴上的位置如图所示,试化简$\sqrt{(b-a)^{2}}$+|2-a|.