题目内容
17. A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.
A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.(1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当它们行驶了7小时时,两车相遇,求乙车的速度及乙车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(3)当两车相距100千米时,求甲车行驶的时间.
分析 (1)设甲车行驶过程中y与x之间的函数解析式为y甲=k1x+b1,分两段代入点的坐标利用待定系数法即可得出结论;
(2)求出当x=7时,y甲的值,再依据“速度=路程÷时间”算出乙车的速度,再由“乙车运动的时间=A、B两城间距离÷乙车的速度”得出x的取值范围,依据数量关系即可得出结论;
(3)设两车之间的距离为W(千米),根据W=|y甲-y乙|得出W关于时间x的函数关系式,令W=100,求出x值即可.
解答 解:(1)设甲车行驶过程中y与x之间的函数解析式为y甲=k1x+b1,
当0≤x≤6时,将点(0,0),(6,600)代入函数解析式得:
$\left\{\begin{array}{l}{0={b}_{1}}\\{600=6{k}_{1}+{b}_{1}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{k}_{1}=100}\\{{b}_{1}=0}\end{array}\right.$,
∴y甲=100x;
当6≤x≤14,将点(6,600),(14,0)代入函数解析式得:
$\left\{\begin{array}{l}{600=6{k}_{1}+{b}_{1}}\\{0=14{k}_{1}+{b}_{1}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{k}_{1}=-75}\\{{b}_{1}=1050}\end{array}\right.$,
∴y甲=-75x+1050.
综上得:y甲=$\left\{\begin{array}{l}{100x(0≤x≤6)}\\{-75x+1050(6≤x≤14)}\end{array}\right.$.
(2)当x=7时,y甲=-75×7+1050=525,
乙车的速度为:525÷7=75(千米/小时).
∵乙车到达B城的时间为:600÷75=8(小时),
∴乙车行驶过程中y乙与x之间的函数解析式为:y乙=75x(0≤x≤8).
(3)设两车之间的距离为W(千米),则W与x之间的函数关系式为:
W=|y甲-y乙|=$\left\{\begin{array}{l}{100x-75x=25x(0≤x≤6)}\\{-75x+1050-75x=-150x+1050(6≤x≤7)}\\{75x-(-75x+1050)=150x-1050(7≤x≤8)}\\{600-(-75x+1050)=75x-450(8≤x≤14)}\end{array}\right.$,
当W=100时,有$\left\{\begin{array}{l}{25x=100(0≤x≤6)}\\{-150x+1050=100(6≤x≤7)}\\{150x-1050=100(7≤x≤8)}\\{75x-450=100(8≤x≤14)}\end{array}\right.$,
解得:x1=4,x2=6$\frac{1}{3}$,x3=7$\frac{2}{3}$.
答:当两车相距100千米时,甲车行驶的时间为4、6$\frac{1}{3}$或7$\frac{2}{3}$小时.
点评 本题考查了一次函数的应用、待定系数法求函数解析式以及解一元一次方程,解题的关键是:(1)利用待定系数法求出函数解析式;(2)结合数量关系找出y乙与x之间的函数解析式;(3)找出关于时间t的一元一次方程.本题属于中档题,难度不大,解决该题型题目时,结合函数图象中点的坐标利用待定系数法求出函数解析式是关键.

| 人数 | 3 | 4 | 2 | 1 |
| 分数 | 80 | 85 | 90 | 95 |
| A. | 85和85 | B. | 85和80 | C. | 95和85 | D. | 85和87.5 |
| A. | 矩形 | B. | 菱形 | ||
| C. | 对角线相等的四边形 | D. | 对角线互相垂直的四边形 |
| A. | 一、二象限 | B. | 三、四象限 | C. | 一、三象限 | D. | 二、四象限 |
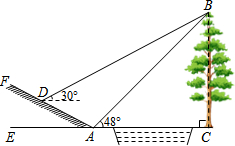 如图所示,小河中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.若斜坡FA的坡比i=1:$\sqrt{3}$,求大树的高度.(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,$\sqrt{3}$≈1.73)
如图所示,小河中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.若斜坡FA的坡比i=1:$\sqrt{3}$,求大树的高度.(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,$\sqrt{3}$≈1.73)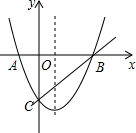 如图,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(-1,0),点C的坐标是(0,-3).
如图,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(-1,0),点C的坐标是(0,-3).