��Ŀ����
18�� ��ͼ����֪��O��0��0����A��-4��-1�����߶�AB��x��ƽ�У���AB=2��������l��y=-x2+mx+n��m��nΪ������������C��0��3����D��3��0��
��ͼ����֪��O��0��0����A��-4��-1�����߶�AB��x��ƽ�У���AB=2��������l��y=-x2+mx+n��m��nΪ������������C��0��3����D��3��0����1����l�Ľ���ʽ����Գ���Ͷ������ꣻ
��2���жϵ�B�Ƿ���l�ϣ���˵�����ɣ�
��3�����߶�AB��ÿ��2����λ�����ٶ�����ƽ�ƣ���ƽ�Ƶ�ʱ��Ϊt���룩��
����l���߶�AB���й����㣬ֱ��д��t��ȡֵ��Χ��
����lͬʱ��ÿ��3����λ�����ٶ�����ƽ�ƣ�l��y�ἰ���Ҳ��ͼ����ֱ��AB�������������㣬��t��ȡֵ��Χ��
���� ��1��ֱ�����ô���ϵ����������κ������ɣ�
��2�����ȵó�B�����꣬�ٴ�����κ�������ʽ�����ó��𰸣�
��3���ٷֱ�ó���������l������Bʱ����������l������Aʱ�����y��ֵ�������ó�t��ȡֵ��Χ��
�ڸ�������ó�����t�IJ���ʽ������ɷ���������𰸣�
��� �⣺��1���ѵ�C��0��3����D��3��0�����������y=-x2+mx+n�У�
��$\left\{\begin{array}{l}n=3\\-{3^2}+3m+n=0\end{array}\right.$��
���$\left\{\begin{array}{l}n=3\\ m=2\end{array}\right.$��
��������l����ʽΪy=-x2+2x+3��
�Գ���Ϊx=1����������Ϊ��1��4����
��2�����ڣ�
��A��-4��-1�����߶�AB��x��ƽ�У�AB=2��
��B��-2��-1����
��x=-2����y=-x2+2x+3����y=-5��-1��
���B����������l�ϣ�
��3����2��t��10�� 
���B��������-2��-1-2t������A��������-4��-1-2t����
��������l������Bʱ����y=-��-2��2+2����-2��+3=-5��
��������l������Aʱ����y=-��-4��2+2����-4��+3=-21��
��������l���߶�AB���й�����ʱ����-21��-1-2t��-5��
��ã�2��t��10��
��ƽ�ƹ����У����C������Ϊ��0��3-3t����������l�Ķ�������Ϊ��1��4-3t����
���ֱ��AB��������l��y�ἰ���Ҳ��ͼ���������������㣬
���� $\left\{\begin{array}{l}-1-2t��3-3t\\-1-2t��4-3t\end{array}\right.$��
��ã�4��t��5��
���� ������Ҫ�����˶��κ����ۺ��Լ�����ʽ��Ľⷨ��֪ʶ����ȷ�������ν�Ϸ����ó�����t�IJ���ʽ�ǽ���ؼ���

 ��ͼ����һ��С��ڷ���Բ���ϣ��ü�����ĸ���ͼ�ǣ�������
��ͼ����һ��С��ڷ���Բ���ϣ��ü�����ĸ���ͼ�ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
| A�� | m=4��n=3 | B�� | m=4��n=4 | C�� | m=3��n=4 | D�� | m=3��n=3 |
| ���� | 3 | 4 | 2 | 1 |
| ���� | 80 | 85 | 90 | 95 |
| A�� | 85��85 | B�� | 85��80 | C�� | 95��85 | D�� | 85��87.5 |
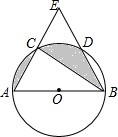 ��ͼ��AB�ǡ�O��ֱ������C��D��Բ�����ȷֵ㣬AC��BD���ӳ��߽��ڵ�E����CE=2�����O����Ӱ���ֵ����Ϊ$\frac{4}{3}$��-$\sqrt{3}$��
��ͼ��AB�ǡ�O��ֱ������C��D��Բ�����ȷֵ㣬AC��BD���ӳ��߽��ڵ�E����CE=2�����O����Ӱ���ֵ����Ϊ$\frac{4}{3}$��-$\sqrt{3}$��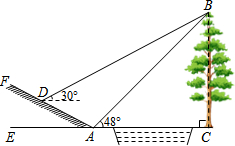 ��ͼ��ʾ��С����ѧ���꼶��ѧ�С��ѡ������ѧУǰ��С�Ӷ�����BC�ĸ߶ȣ�������б����D����ô�������B��������30�㣬����������������6�����µ�A������A����ô�������B��������48�㣮��б��FA���±�i=1��$\sqrt{3}$��������ĸ߶ȣ�����������������ο����ݣ�sin48���0.74��cos48���0.67��tan48���1.11��$\sqrt{3}$��1.73��
��ͼ��ʾ��С����ѧ���꼶��ѧ�С��ѡ������ѧУǰ��С�Ӷ�����BC�ĸ߶ȣ�������б����D����ô�������B��������30�㣬����������������6�����µ�A������A����ô�������B��������48�㣮��б��FA���±�i=1��$\sqrt{3}$��������ĸ߶ȣ�����������������ο����ݣ�sin48���0.74��cos48���0.67��tan48���1.11��$\sqrt{3}$��1.73��