题目内容
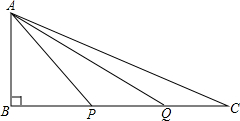 如图,△ABC中,∠ABC=90°,点P、Q分别是边BC上的两点,连接AP、AQ,且AB=BP=PQ=QC=1,问图中是否有相似三角形?并说明理由.
如图,△ABC中,∠ABC=90°,点P、Q分别是边BC上的两点,连接AP、AQ,且AB=BP=PQ=QC=1,问图中是否有相似三角形?并说明理由.考点:相似三角形的判定
专题:
分析:利用勾股定理得出AP的长,再利用相似三角形的判定方法得出即可.
解答:解:△APQ∽△CPA,
理由:∵AB=BP=1,
在直角三角形ABP中,
AP=
,
∵PQ=QC=1,
∴PC=2,
∴AP:CP=PQ:PA,
又∵∠APC=∠CPA,
∴△APQ∽△CPA.
理由:∵AB=BP=1,
在直角三角形ABP中,
AP=
| 2 |
∵PQ=QC=1,
∴PC=2,
∴AP:CP=PQ:PA,
又∵∠APC=∠CPA,
∴△APQ∽△CPA.
点评:此题主要考查了相似三角形的判定,得出对应边的比值是解题关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
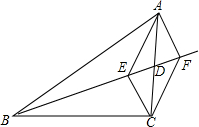 如图,BD是△ABC的中线,CE⊥BD于点E,AF⊥BD交BD的延长线于点F.
如图,BD是△ABC的中线,CE⊥BD于点E,AF⊥BD交BD的延长线于点F. 已知:如图,Rt△ABC中,AC=4,BC=3,DE∥AB.当△CDE的面积与四边形DABE的面积相等时,求△CDE的周长.
已知:如图,Rt△ABC中,AC=4,BC=3,DE∥AB.当△CDE的面积与四边形DABE的面积相等时,求△CDE的周长.