题目内容
 已知:如图,Rt△ABC中,AC=4,BC=3,DE∥AB.当△CDE的面积与四边形DABE的面积相等时,求△CDE的周长.
已知:如图,Rt△ABC中,AC=4,BC=3,DE∥AB.当△CDE的面积与四边形DABE的面积相等时,求△CDE的周长.考点:相似三角形的判定与性质
专题:
分析:由DE∥AB可得△CDE∽△CAB,设△CDE的面积为S,则四边形DABE的面积也为S,则△CAB的面积为2S,所以相似比为
,结合以
=
=
=
=
,可求出CD、CE、DE的长,进一步求出周长即可.
| ||
| 2 |
| CD |
| CA |
| CE |
| CB |
| DE |
| AB |
|
| ||
| 2 |
解答:解:
Rt△ABC中,AC=4,BC=3,所以AB=5,
设△CDE的面积为S,则四边形DABE的面积也为S,则△CAB的面积为2S,
又DE∥AB,所以有△CDE∽△CAB,
所以
=
=
=
=
,
且AC=4,BC=3,所以可分别求得CD=2
,CE=
,DE=
,
所以△CDE的周长为:CD+CE+DE=2
+
+
=6
.
Rt△ABC中,AC=4,BC=3,所以AB=5,
设△CDE的面积为S,则四边形DABE的面积也为S,则△CAB的面积为2S,
又DE∥AB,所以有△CDE∽△CAB,
所以
| CD |
| CA |
| CE |
| CB |
| DE |
| AB |
|
| ||
| 2 |
且AC=4,BC=3,所以可分别求得CD=2
| 2 |
3
| ||
| 2 |
5
| ||
| 2 |
所以△CDE的周长为:CD+CE+DE=2
| 2 |
3
| ||
| 2 |
5
| ||
| 2 |
| 2 |
点评:本题主要考查三角形相似的判定和性质的应用,解题的关键是由面积相等求出两三角形的相似比.

练习册系列答案
相关题目
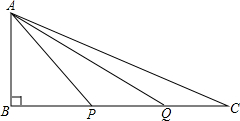 如图,△ABC中,∠ABC=90°,点P、Q分别是边BC上的两点,连接AP、AQ,且AB=BP=PQ=QC=1,问图中是否有相似三角形?并说明理由.
如图,△ABC中,∠ABC=90°,点P、Q分别是边BC上的两点,连接AP、AQ,且AB=BP=PQ=QC=1,问图中是否有相似三角形?并说明理由.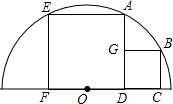 四边形ADFE和四边形BCDG都为正方形,且点F、D、C在半圆O的直径上,点E、A、B在半圆O的圆弧上,若小正方形边长为4cm,求该半圆的半径.
四边形ADFE和四边形BCDG都为正方形,且点F、D、C在半圆O的直径上,点E、A、B在半圆O的圆弧上,若小正方形边长为4cm,求该半圆的半径. 在△ABC中,M是BC边的中点,D是AC上一点,BD与AM交于点E,且DA=DE.求证:BE=AC.
在△ABC中,M是BC边的中点,D是AC上一点,BD与AM交于点E,且DA=DE.求证:BE=AC. 如图,在平面直角坐标系xOy中,∠MAN=45°,顶点A的坐标为(-2
如图,在平面直角坐标系xOy中,∠MAN=45°,顶点A的坐标为(-2