题目内容
12.观察下列各式:13=1=$\frac{1}{4}$×12×22;
13+23=9=$\frac{1}{4}$×22×32;
13+23+33=36=$\frac{1}{4}$×32×42;
…
(1)猜想填空:13+23+33+…+n3=$\frac{1}{4}$×n2×(n+1)2.
(2)若13+23+33+…+n3=$\frac{1}{4}$×2402.试求n的值.
分析 (1)根据已给3个等式知,连续整数的立方和等于$\frac{1}{4}$×最后一整数平方×比最后一整数大1的数的平方,列式即可;
(2)利用(1)中结论,列出方程可求得n的值.
解答 解:(1)∵13=1=$\frac{1}{4}$×12×22=$\frac{1}{4}$×12×(1+1)2,
13+23=9=$\frac{1}{4}$×22×32=$\frac{1}{4}$×22×(2+1)2,
13+23+33=36=$\frac{1}{4}$×32×42=$\frac{1}{4}$×32×(3+1)2,
13+23+33+43=64=$\frac{1}{4}$×42×52=$\frac{1}{4}$×42×(4+1)2,
…,
∴13+23+33+…+n3=$\frac{1}{4}$n2(n+1)2;
(2)根据题意,得:$\frac{1}{4}$×2402=$\frac{1}{4}$n2(n+1)2,即n(n+1)=240,
解得:n=15或n=-16(舍).
故答案为:(1)n,(n+1).
点评 本题是对数字变化规律的考查,正确观察已知的式子的特点,得到规律是解决本题的关键.

练习册系列答案
相关题目
2.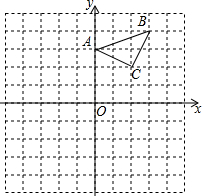 如图,已知△ABC在平面直角坐标系中,点A的坐标为(0,3),若以点B为位似中心,在平面直角坐标系内画出△A′BC′,使得△A′BC′与△ABC位似,且相似比为2:1,则点C′的坐标为( )
如图,已知△ABC在平面直角坐标系中,点A的坐标为(0,3),若以点B为位似中心,在平面直角坐标系内画出△A′BC′,使得△A′BC′与△ABC位似,且相似比为2:1,则点C′的坐标为( )
 如图,已知△ABC在平面直角坐标系中,点A的坐标为(0,3),若以点B为位似中心,在平面直角坐标系内画出△A′BC′,使得△A′BC′与△ABC位似,且相似比为2:1,则点C′的坐标为( )
如图,已知△ABC在平面直角坐标系中,点A的坐标为(0,3),若以点B为位似中心,在平面直角坐标系内画出△A′BC′,使得△A′BC′与△ABC位似,且相似比为2:1,则点C′的坐标为( )| A. | (0,0) | B. | (0,1) | C. | (1,-1) | D. | (1,0) |
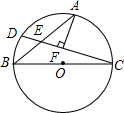 如图,BC是⊙O的直径,点A是$\widehat{BC}$的中点,D为$\widehat{AB}$上一点,DC交AB于E,AF⊥CD于F,AF=2EF,求证:AE=BE.
如图,BC是⊙O的直径,点A是$\widehat{BC}$的中点,D为$\widehat{AB}$上一点,DC交AB于E,AF⊥CD于F,AF=2EF,求证:AE=BE.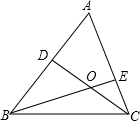 如图,在△ABC中,D为AB的中点,E为AC上一点,CE=$\frac{1}{3}$AC,BE,CD交于点O,OE=2,求BE的长.
如图,在△ABC中,D为AB的中点,E为AC上一点,CE=$\frac{1}{3}$AC,BE,CD交于点O,OE=2,求BE的长.