题目内容
3．
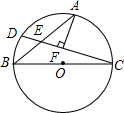如图，BC是⊙O的直径，点A是$\widehat{BC}$的中点，D为$\widehat{AB}$上一点，DC交AB于E，AF⊥CD于F，AF=2EF，求证：AE=BE．
分析 连接AC，由BC是⊙O的直径，得到∠BAC=90°，由已知条件得到AB=AC，通过△AEF∽△ACE，得到$\frac{AE}{AC}=\frac{AF}{EF}$，即可得到结论．
解答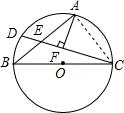 
证明：连接AC，
∵BC是⊙O的直径，
∴∠BAC=90°，
∵点A是$\widehat{BC}$的中点，
∴$\widehat{AB}=\widehat{AC}$，
∴AB=AC，
∵AF⊥CD于F，
∴∠AFE=∠EAC=90°，
∵∠AEF=∠AEC，
∴△AEF∽△ACE，
∴$\frac{AE}{AC}=\frac{AF}{EF}$，
∵AF=2EF，
∴AC=2AE，
∴AB=2AE，
∴AE=BE．
点评 本题考查了相似三角形的判定和性质，圆周角定理，连接AC，构造相似三角形是解题的关键．
练习册系列答案
相关题目
13．某区从参加地理学业水平考试的8000名学生中，随机抽取了部分学生的成绩作为样本，为了节省时间，先将样本分成甲、乙两组，分别进行分析，得到下表；随后汇总整个样本数据，得到部分结果，绘制成如下统计图．
（注：A：优秀（≥90分）、B：良好（≥70分且＜90分）、C：及格（≥60分且＜70分）、D：不及格（＜60分））
表一
请根据图和表所示信息回答下列问题：
（1）样本中，学生地理学成绩平均分为B分，中位数在B内（填等第），众数是
B（填等第）．A占的百分比是30%，C占的百分比是15%．
（2）补全条形统计图．
（3）成绩不低于60的为合格，估计这8000名学生的合格人数．
（注：A：优秀（≥90分）、B：良好（≥70分且＜90分）、C：及格（≥60分且＜70分）、D：不及格（＜60分））
表一
| 甲组 | 乙组 | |
| 人数（人） | 120 | 80 |
| 平均分（分） | 88 | 83 |
（1）样本中，学生地理学成绩平均分为B分，中位数在B内（填等第），众数是
B（填等第）．A占的百分比是30%，C占的百分比是15%．
（2）补全条形统计图．
（3）成绩不低于60的为合格，估计这8000名学生的合格人数．
如图是某几何体的三视图，根据图中数据，求得该几何体的体积为70π．（结果保留π）
在?ABCD中，延长DA至E，延长BC至F，使AE=CF，连结EF分别交AB和CD于G、H．求证：BG=DH．
18．某校九（1）班同学积极参加社团活动，每人均参加篮球、书法、舞蹈和象棋其中的一项，小明同学调查后，整理相关数据并制作了两个不完整的统计图：
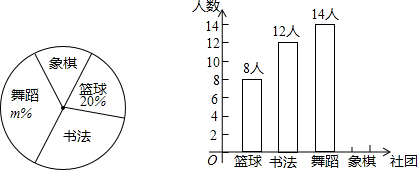
根据以上信息解答下列问题：
（1）请补全条形统计图，并直接写出扇形统计图中的m=35
（2）学校对该班社团活动进行测评，各社团的平均得分如表：
求九（1）班社团测评的平均分．
根据以上信息解答下列问题：
（1）请补全条形统计图，并直接写出扇形统计图中的m=35
（2）学校对该班社团活动进行测评，各社团的平均得分如表：
| 社团 | 篮球 | 书法 | 舞动 | 象棋 |
| 平均分 | 4 | 4.5 | 3 | 4 |
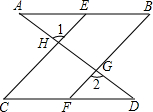已知，如图，直线AD分别与EC，BF分别相交于点H，G，已知∠1=∠2，∠B=∠C．