题目内容
2.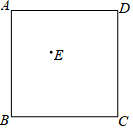 如图,在正方形ABCD内任取一点E,连结AE、BE,在△ABE外分别以AE、BE为边作正方形AEMN和EBFG.
如图,在正方形ABCD内任取一点E,连结AE、BE,在△ABE外分别以AE、BE为边作正方形AEMN和EBFG.(1)按题意,在图中补全符合条件的图形.
(2)在补全的图形中,连结CF,求证:AN∥CF.
分析 (1)根据要求画出图形即可;
(2)延长AE交BC于O,交CF于K.只要证明△ABE≌△CBF,推出∠BAE=∠BCF,由∠BAE+∠AOB=90°,∠AOB=∠COK,推出∠COK+∠BCF=90°,推出∠AKC=90°,推出AE⊥CF,延长即可解决问题;
解答 (1)解:补全的图形如图所示.
(2)证明:延长AE交BC于O,交CF于K.
∵四边形ABCD,四边形EBFG是正方形,
∴AB=BC,EB=BF,∠ABC=∠EBF=90°,
∴∠ABE=∠CBF,
∴△ABE≌△CBF,
∴∠BAE=∠BCF,
∵∠BAE+∠AOB=90°,∠AOB=∠COK,
∴∠COK+∠BCF=90°,
∴∠AKC=90°,
∴AE⊥CF,∵AN⊥AE,
∴AN∥CF.
点评 本题考查正方形的性质、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
12.2016年春节临近,武汉掀起购物狂潮,现有甲、乙、丙三个商场开展的促销活动如表所示:
根据以上活动信息,解决以下问题:
(1)三个商场同时出售一件标价290元的上一和一条标价270元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场?完成表后就可以做出选择
(2)黄先生发现在甲、乙商场同时出售一件标价380元的上衣和一条标价300多元的裤子,最后付款额也一样,请问这条裤子的标价是多少元?
(3)丙商场又推出“先打折”,“再满100元减50元”的活动.张先生买了一件标价为630元的上衣,张先生发现竟然比没打折前多付了20元钱,问丙商场先打了多少折后再参加活动?(结果精确到0.01)
| 商场 | 优惠活动 |
| 甲 | 全场按标价的6折销售 |
| 乙 | 实行“满100元送100元的购物券”的优惠,购物券可以在再购买时冲抵现金 (比如:顾客购衣服220元,赠券200元,再购买裤子时可冲抵现金,不再送券) |
| 丙 | 实行“满100元减50元的优惠”(比如:某顾客购物220元,他只需付款120元) |
(1)三个商场同时出售一件标价290元的上一和一条标价270元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场?完成表后就可以做出选择
| 商场 | 甲商场 | 乙商场 | 丙商场 |
| 实际付款(元) | 336 | 360 | 310 |
(3)丙商场又推出“先打折”,“再满100元减50元”的活动.张先生买了一件标价为630元的上衣,张先生发现竟然比没打折前多付了20元钱,问丙商场先打了多少折后再参加活动?(结果精确到0.01)
13.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
11.某个公司有15名工作人员,他们的月工资情况如表.则该公司所有工作人员的月工资的平均数、中位数和众数分别是( )
| 职务 | 经理 | 副经理 | 职员 |
| 人数 | 1 | 2 | 12 |
| 月工资(元) | 5 000 | 2 000 | 800 |
| A. | 520,2 000,2 000 | B. | 2 600,800,800 | C. | 1 240,2 000,800 | D. | 1 240,800,800 |
12.关于函数y=2x-3,下列结论正确的是( )
| A. | 图象必经过(0,-3) | B. | 图象不过第三象限 | ||
| C. | y随x的增大而减小 | D. | 当x>1.5时,y<0 |
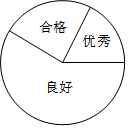 某校学生参加某项数学检测的成绩被分为优秀、良好、合格三个等级,其人数比为2:7:3,如图所示的扇形图表示上述分布情况.
某校学生参加某项数学检测的成绩被分为优秀、良好、合格三个等级,其人数比为2:7:3,如图所示的扇形图表示上述分布情况.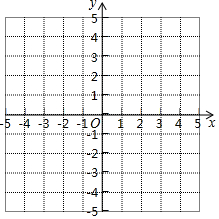 已知△ABC的三个顶点的坐标分别是A(-2,3),点B(0,1),点C(2,2).
已知△ABC的三个顶点的坐标分别是A(-2,3),点B(0,1),点C(2,2).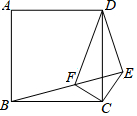 如图,已知在正方形ABCD外取一点E,连接CE、BE、DE.过点C作CE的垂线交BE于点F.CE=CF=1,DF=$\sqrt{6}$.下列结论:①△BCF≌△DCE;②EB⊥ED;③点D到直线CE的距离为2;④S四边形DECF=$\sqrt{2}$+$\frac{1}{2}$.其中正确结论的序号是①②④.
如图,已知在正方形ABCD外取一点E,连接CE、BE、DE.过点C作CE的垂线交BE于点F.CE=CF=1,DF=$\sqrt{6}$.下列结论:①△BCF≌△DCE;②EB⊥ED;③点D到直线CE的距离为2;④S四边形DECF=$\sqrt{2}$+$\frac{1}{2}$.其中正确结论的序号是①②④.