题目内容
14.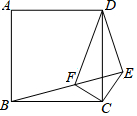 如图,已知在正方形ABCD外取一点E,连接CE、BE、DE.过点C作CE的垂线交BE于点F.CE=CF=1,DF=$\sqrt{6}$.下列结论:①△BCF≌△DCE;②EB⊥ED;③点D到直线CE的距离为2;④S四边形DECF=$\sqrt{2}$+$\frac{1}{2}$.其中正确结论的序号是①②④.
如图,已知在正方形ABCD外取一点E,连接CE、BE、DE.过点C作CE的垂线交BE于点F.CE=CF=1,DF=$\sqrt{6}$.下列结论:①△BCF≌△DCE;②EB⊥ED;③点D到直线CE的距离为2;④S四边形DECF=$\sqrt{2}$+$\frac{1}{2}$.其中正确结论的序号是①②④.
分析 根据正方形的性质、全等三角形的判定和性质、勾股定理等知识一一判断即可.
解答 解:在正方形ABCD中,
BC=CD,∠BCD=90°,
∵∠EACF90°,
∴∠BCF=∠DCE,
在△BCF与△DCE中,
$\left\{\begin{array}{l}{BC=CD}\\{∠BCE=∠DCF}\\{CF=CE}\end{array}\right.$,
∴△BCE≌△DCF(SAS),
故①正确;
∵△BCF≌△DCE,
∴∠CBF=∠CDE,
∴∠DEB=∠BCD=90°,
∴BE⊥ED,
故②正确,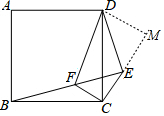
过点D作DM⊥CE,交CE的延长线于点M,
∵∠ECF=90°,
FC=EC=1,
∴∠CEF=45°,
∵∠DEM+∠CEB=90°,
∴∠DEM=∠EDM=45°,
∴EM=DM,
∴由勾股定理可求得:EF=$\sqrt{2}$,
∵DF=$\sqrt{6}$,
∴由勾股定理可求得:DE=2,
∵EF2+BF2=2BF2=BE2,
∴DM=EM=$\sqrt{2}$,故③错误,
∵△BCF≌△ADCE,
∴S△BCF=S△DCE,
∴S△DCE+S△DCF
=S△ECF+S△DEF
=S△AEP+S△PEB
=$\frac{1}{2}$+$\sqrt{2}$,故④正确,
故答案为①②④
点评 本题考查四边形的综合问题,涉及全等三角形的性质与判定,勾股定理,三角形面积公式等知识内容,综合程度高,需要学生灵活运用知识解答.

练习册系列答案
相关题目
4.点P(2m+6,m-1)在第三象限,则m的取值范围是( )
| A. | m<-3 | B. | m<1 | C. | m>-3 | D. | -3<m<1 |
9.下列各点中,在第二象限的点是( )
| A. | (-1,4) | B. | (1,-4) | C. | (-1,-4) | D. | (1,4) |
6.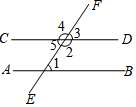 如图,下列判断中正确的是( )
如图,下列判断中正确的是( )
 如图,下列判断中正确的是( )
如图,下列判断中正确的是( )| A. | 如果∠3+∠2=180°,那么AB∥CD | B. | 如果∠1+∠3=180°,那么AB∥CD | ||
| C. | 如果∠2=∠4,那么AB∥CD | D. | 如果∠1=∠5,那么AB∥CD |
3.已知|x|=3,y=2,且x>y,则x+y的值为( )
| A. | -5 | B. | -1 | C. | 5或-1 | D. | 5 |
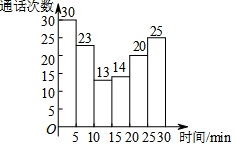 张涛同学统计了他家5月份的长途电话明细清单,按通话时间画出直方图(如图).通话时间不少于15min且不足25min的,共有( )次.
张涛同学统计了他家5月份的长途电话明细清单,按通话时间画出直方图(如图).通话时间不少于15min且不足25min的,共有( )次. 如图,在正方形ABCD内任取一点E,连结AE、BE,在△ABE外分别以AE、BE为边作正方形AEMN和EBFG.
如图,在正方形ABCD内任取一点E,连结AE、BE,在△ABE外分别以AE、BE为边作正方形AEMN和EBFG. 如图是一次函数y=mx+n的图象,则关于x的不等式mx+n>2的解集是x>0.
如图是一次函数y=mx+n的图象,则关于x的不等式mx+n>2的解集是x>0.