题目内容
12.阅读并解答问题:对于一个一般的二元一次方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$,探索其解的情况,先将把两个二元一次方程都化成一次函数表达式,如:$\left\{\begin{array}{l}{y=-\frac{{b}_{1}}{{a}_{1}}x+\frac{{c}_{1}}{{a}_{1}}}\\{y=-\frac{{b}_{2}}{{a}_{2}}x+\frac{{c}_{2}}{{a}_{2}}}\end{array}\right.$.(1)当-$\frac{{b}_{1}}{{a}_{1}}$≠-$\frac{{b}_{2}}{{a}_{2}}$,即$\frac{{a}_{1}}{{a}_{2}}$≠$\frac{{b}_{1}}{{b}_{2}}$时,二元一次方程组有唯一的解;
(2)当-$\frac{{b}_{1}}{{a}_{1}}$=-$\frac{{b}_{2}}{{a}_{2}}$且$\frac{{c}_{1}}{{a}_{1}}$≠$\frac{{c}_{2}}{{a}_{2}}$,即$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$≠$\frac{{c}_{1}}{{c}_{2}}$时,二元一次方程组无解;
(3)当-$\frac{{b}_{1}}{{a}_{1}}$=-$\frac{{b}_{2}}{{a}_{2}}$且$\frac{{c}_{1}}{{a}_{1}}$=$\frac{{c}_{2}}{{a}_{2}}$,即$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$=$\frac{{c}_{1}}{{c}_{2}}$时,二元一次方程组有无数个解.
问题:当k为何值时,二元一次方程组:$\left\{\begin{array}{l}{kx+2y=2}\\{3x-5y=2}\end{array}\right.$无解?
分析 首先把两个方程化为一次函数y=kx+b形式的形式,再根据材料可得-$\frac{k}{2}$=$\frac{3}{5}$时,方程组无解,然后求出k的值即可.
解答 解:kx+2y=2可化为y=-$\frac{k}{2}$x+1,
3x-5y=2可化为y=$\frac{3}{5}$x-$\frac{2}{5}$,
∵二元一次方程组:$\left\{\begin{array}{l}{kx+2y=2}\\{3x-5y=2}\end{array}\right.$无解,
∴-$\frac{k}{2}$=$\frac{3}{5}$,
解得:k=-$\frac{6}{5}$.
点评 此题主要考查了一次函数与二元一次方程组,关键是正确理解题目所给材料的意思.

练习册系列答案
相关题目
3.若y=(a-1)x${\;}^{{a}^{2}}$-2是反比例函数,则a的取值为( )
| A. | 1 | B. | -1 | C. | ±1 | D. | ±$\sqrt{3}$ |
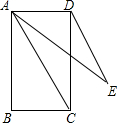 如图,矩形ABCD,AB=2$\sqrt{3}$,AC=4,将对角线AC绕点A旋转得到线段AE,连接DE,DE∥AC,则线段DE=-1+$\sqrt{13}$.
如图,矩形ABCD,AB=2$\sqrt{3}$,AC=4,将对角线AC绕点A旋转得到线段AE,连接DE,DE∥AC,则线段DE=-1+$\sqrt{13}$. 如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为64和42,则△EDF的面积为12.
如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为64和42,则△EDF的面积为12. 某城市采用分段计费的方法来计算电费,月用电量x度与相应电费y元之间的函数关系如图:
某城市采用分段计费的方法来计算电费,月用电量x度与相应电费y元之间的函数关系如图: