题目内容
4.已知抛物线y=$\frac{1}{2}$x2-4x+6与x轴交于A,B两点,与y轴交于点C.(1)写出抛物线的开口方向、对称轴和顶点;
(2)求△ABC的面积.
分析 (1)把抛物线的一般式写成顶点坐标式,进而得到答案;
(2)令y=0,求出x的值,令x=0,求出y的值,即可求出△ABC的面积.
解答 解:(1)抛物线y=$\frac{1}{2}$x2-4x+6=$\frac{1}{2}$(x2-8x+16)-2=$\frac{1}{2}$(x-4)2-2,
即抛物线的开口向上,对称轴为直线x=4,顶点坐标为(4,-2);
(2)令y=$\frac{1}{2}$x2-4x+6=0,
解得x1=2,x2=6,
则AB=4,
令x=0,y=6,
则OC=6,
即△ABC的面积=$\frac{1}{2}$×4×6=12.
点评 本题考查了抛物线与x轴的交点.解题时需要熟悉二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象与x轴的交点与一元二次方程ax2+bx+c=0根之间的关系.

练习册系列答案
相关题目
 如图,数轴上A点表示的数是a,B点表示的数是b,点A在点B的右边
如图,数轴上A点表示的数是a,B点表示的数是b,点A在点B的右边 如图,AB是⊙O的直径,CD切⊙O于C,AD⊥CD于D.求证:AC平分∠DAB.
如图,AB是⊙O的直径,CD切⊙O于C,AD⊥CD于D.求证:AC平分∠DAB.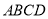 中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,已知a=2b=6c,其面积是_________________________.(用含c的代数式表示)
中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,已知a=2b=6c,其面积是_________________________.(用含c的代数式表示)