题目内容
某商场以每件20元的价格购进一种商品，试销中发现，这种商品每天的销售量m（件）与每件的销售价x（元）满足关系：m=140-2x．如果商场要想每天获得800元的销售利润，又让顾客得到实惠，每件商品的售价应定为多少？
考点：一元二次方程的应用
专题：销售问题
分析：一天的利润=（售价-进价）×销售量，据此列出方程求解即可．
解答：解：设每件商品的售价应定为x元，由题意，得
（x-20）（140-2x）=800，
整理，得x2-90x+1800=0，
解得x1=30，x2=60．
∵要让顾客得到实惠，
∴x=30，
答：每件商品的售价应定为30元．
（x-20）（140-2x）=800，
整理，得x2-90x+1800=0，
解得x1=30，x2=60．
∵要让顾客得到实惠，
∴x=30，
答：每件商品的售价应定为30元．
点评：考查一元二次方程的应用；得到一天的利润的等量关系是解决本题的关键．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
方程x2-6x+9=0的根的情况是（ ）
| A、没有实数根 |
| B、有且仅有一个实数根 |
| C、有两个相等的实数根 |
| D、有两个不相等的实数根 |
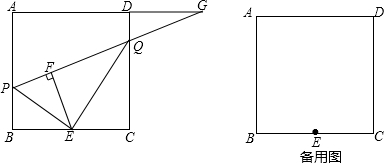
如图，已知∠A=∠B=25°，若∠A+∠B+∠BCA=180°，求∠ACE．