题目内容
12. 如图,菱形ABCD的边长为4,∠ABC=60°,点E、F分别为AO、AB的中点,则EF的长度为( )
如图,菱形ABCD的边长为4,∠ABC=60°,点E、F分别为AO、AB的中点,则EF的长度为( )| A. | 4 | B. | 3 | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
分析 先根据菱形的性质得出∠ABO=$\frac{1}{2}$∠ABC=30°,由30°的直角三角形的性质得出OA=$\frac{1}{2}$AB=2,再根据勾股定理求出OB,然后证明EF为△AOB的中位线,根据三角形中位线定理即可得出结果.
解答 解:∵四边形ABCD是菱形,
∴AC⊥BD,∠ABO=$\frac{1}{2}$∠ABC=30°,
∴OA=$\frac{1}{2}$AB=2,
∴OB=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∵点E、F分别为AO、AB的中点,
∴EF为△AOB的中位线,
∴EF=$\frac{1}{2}$OB=$\sqrt{3}$.
故选:D.
点评 本题考查了矩形的性质、勾股定理、含30°角的直角三角形的性质以及三角形中位线定理;根据勾股定理求出OB和证明三角形中位线是解决问题的关键.

练习册系列答案
相关题目
2. 如图,∠AOB是平角,OD、OE分别是∠AOC、∠BOC平分线,∠DOE等于( )
如图,∠AOB是平角,OD、OE分别是∠AOC、∠BOC平分线,∠DOE等于( )
 如图,∠AOB是平角,OD、OE分别是∠AOC、∠BOC平分线,∠DOE等于( )
如图,∠AOB是平角,OD、OE分别是∠AOC、∠BOC平分线,∠DOE等于( )| A. | 105° | B. | 100° | C. | 90° | D. | 80° |
3.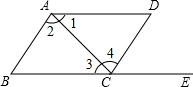 如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
 如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )| A. | ∠1=∠3 | B. | ∠D=∠DCE | C. | ∠2=∠4 | D. | ∠D+∠BCD=180° |
 如图是一束平行光线从教室窗户射入的平面示意图,BC=1,NC=$\frac{4}{3}$,BN=$\frac{5}{3}$,AB=3.5,MN=$\frac{14}{3}$,求AM的长度.
如图是一束平行光线从教室窗户射入的平面示意图,BC=1,NC=$\frac{4}{3}$,BN=$\frac{5}{3}$,AB=3.5,MN=$\frac{14}{3}$,求AM的长度.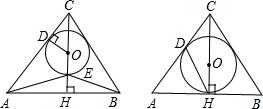
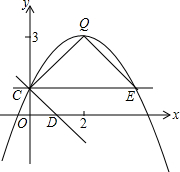 如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC
如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC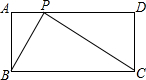 如图,在长方形ABCD中,AB=2$\sqrt{5}$cm,BC=4$\sqrt{5}$cm.点P以$\sqrt{5}$cm/s的速度在长方形边上从点A出发,沿A-D-C的路径运动,到点C停止.
如图,在长方形ABCD中,AB=2$\sqrt{5}$cm,BC=4$\sqrt{5}$cm.点P以$\sqrt{5}$cm/s的速度在长方形边上从点A出发,沿A-D-C的路径运动,到点C停止.