题目内容
4.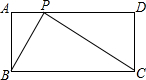 如图,在长方形ABCD中,AB=2$\sqrt{5}$cm,BC=4$\sqrt{5}$cm.点P以$\sqrt{5}$cm/s的速度在长方形边上从点A出发,沿A-D-C的路径运动,到点C停止.
如图,在长方形ABCD中,AB=2$\sqrt{5}$cm,BC=4$\sqrt{5}$cm.点P以$\sqrt{5}$cm/s的速度在长方形边上从点A出发,沿A-D-C的路径运动,到点C停止.(1)求2s后三角形BAP的面积;
(2)求5s后三角形BCP的面积.
分析 (1)2s后,点P在边AD上,根据三角形的面积公式进行解答即可.
(2)5s后,点P在边CD上,根据三角形的面积公式进行解答.
解答 解:(1)在矩形ABCD中,AB=2$\sqrt{5}$cm,∠A=90°.
2s后三角形BAP的面积为:$\frac{1}{2}$AB•AP=$\frac{1}{2}$×2$\sqrt{5}$×2×$\sqrt{5}$=10(cm2),即2s后三角形BAP的面积是10cm2;
(2)在矩形ABCD中,AB=CD=2$\sqrt{5}$cm,AD=BC=4$\sqrt{5}$cm,DC⊥BC.
5s后,CP=(2$\sqrt{5}$+4$\sqrt{5}$)-5×$\sqrt{5}$=$\sqrt{5}$(cm).
5s后三角形BCP的面积为:$\frac{1}{2}$AB•CP=$\frac{1}{2}$×2$\sqrt{5}$×$\sqrt{5}$=5(cm2),即2s后三角形BAP的面积是5cm2.
点评 本题考查了矩形的性质.此题利用了矩形的对边相等且四个内角为直角的性质来解题.

练习册系列答案
相关题目
14.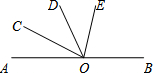 如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,则∠BOE的度数为( )
如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,则∠BOE的度数为( )
 如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,则∠BOE的度数为( )
如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,则∠BOE的度数为( )| A. | 360°-4α | B. | 180°-4α | C. | α | D. | 2α-60° |
12. 如图,菱形ABCD的边长为4,∠ABC=60°,点E、F分别为AO、AB的中点,则EF的长度为( )
如图,菱形ABCD的边长为4,∠ABC=60°,点E、F分别为AO、AB的中点,则EF的长度为( )
 如图,菱形ABCD的边长为4,∠ABC=60°,点E、F分别为AO、AB的中点,则EF的长度为( )
如图,菱形ABCD的边长为4,∠ABC=60°,点E、F分别为AO、AB的中点,则EF的长度为( )| A. | 4 | B. | 3 | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
13. 如图所示的作图痕迹作的是( )
如图所示的作图痕迹作的是( )
 如图所示的作图痕迹作的是( )
如图所示的作图痕迹作的是( )| A. | 线段的垂直平分线 | B. | 过一点作已知直线的垂线 | ||
| C. | 一个角的平分线 | D. | 作一个角等于已知角 |
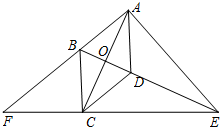 菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.
菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE. 如图,?ABCD的对角线AC、BD相交于点O,指出图中各对相等的线段.
如图,?ABCD的对角线AC、BD相交于点O,指出图中各对相等的线段.