题目内容
1.已知关于x的一元二次方程x2-2x+3m-1=0有两个实数根分别为x1,x2.(1)求m的取值范围;
(2)若|x1-x2|=1,求m的值;
(3)将m表示为x的二次函数,求该二次函数的最大(或最小)值.
分析 (1)根据关于x的一元二次方程x2-2x+3m-1=0有两个实数根分别为x1,x2,得出b2-4ac≥0,然后代入求解即可;
(2)根据根与系数的关系得出x1+x2=2,x1x2=3m-1,再把|x1-x2|=1进行变形,即可求出m的值;
(3)根据题意得出m=-x2+2x+1=-(x-1)2+2,再根据二次函数的性质即可得出答案.
解答 解:(1)∵x2-2x+3m-1=0有两个实数根分别为x1和x2,
∴b2-4ac=(-2)2-4(3m-1)≥0,
∴m≤$\frac{2}{3}$;
(2)∵x1+x2=2,x1x2=3m-1,
∴|x1-x2|2=|(x1+x2)2-4x1x2|=|4-4(3m-1)|=4|2-3m|=1,
∴2-3m=±$\frac{1}{4}$,
∴m=$\frac{7}{12}$或$\frac{3}{4}$(不合题意,舍去),
∴m=$\frac{7}{12}$;
(3)∵m=-x2+2x+1=-(x-1)2+2,
∴当x=1时,m有最大值,最大值是2.
点评 本题考查了根的判别式、根与系数的关系与二次函数的最值问题,一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
12. 如图,菱形ABCD的边长为4,∠ABC=60°,点E、F分别为AO、AB的中点,则EF的长度为( )
如图,菱形ABCD的边长为4,∠ABC=60°,点E、F分别为AO、AB的中点,则EF的长度为( )
 如图,菱形ABCD的边长为4,∠ABC=60°,点E、F分别为AO、AB的中点,则EF的长度为( )
如图,菱形ABCD的边长为4,∠ABC=60°,点E、F分别为AO、AB的中点,则EF的长度为( )| A. | 4 | B. | 3 | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
6.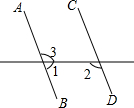 如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是( )
如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是( )
 如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是( )
如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是( )| A. | ∠2=70° | B. | ∠2=100° | C. | ∠2=110° | D. | ∠3=110° |
13. 如图所示的作图痕迹作的是( )
如图所示的作图痕迹作的是( )
 如图所示的作图痕迹作的是( )
如图所示的作图痕迹作的是( )| A. | 线段的垂直平分线 | B. | 过一点作已知直线的垂线 | ||
| C. | 一个角的平分线 | D. | 作一个角等于已知角 |
10.数轴上表示-5的点到原点的距离为( )
| A. | 5 | B. | -5 | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |